已知抛物线抛物线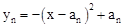（n为正整数，且0<a₁<a₂<…<a_n）与x轴的交点为A_n-1（b_n-1,0）和A_n(b_n，0)，当n=1时，第1条抛物线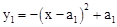与x轴的交点为A₀（0，0）和A₁（b₁，0），其他依此类推．
（1）求a₁,b₁的值及抛物线y₂的解析式；
（2）抛物线y₃的顶点坐标为（       ，       ）；
依此类推第n条抛物线y_n的顶点坐标为（       ，       ）;
所有抛物线的顶点坐标满足的函数关系是       ；
（3）探究下列结论：
①若用A_n-1A_n表示第n条抛物线被x轴截得得线段长，直接写出A₀A₁的值，并求出A_n-1A_n；
②是否存在经过点A（2，0）的直线和所有抛物线都相交，且被每一条抛物线截得得线段的长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．

如图①，已知抛物线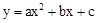经过点A（0，3），B（3，0），C（4，3）．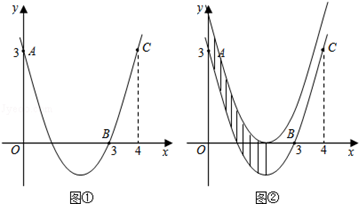

（1）求抛物线的函数表达式；
（2）求抛物线的顶点坐标和对称轴；
（3）把抛物线向上平移，使得顶点落在x轴上，直接写出两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影部分）．

已知抛物线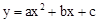与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．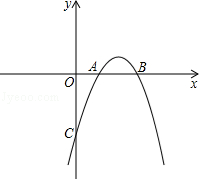

（1）求抛物线的解析式和顶点坐标；
（2）请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=﹣x上，并写出平移后抛物线的解析式．

如图，已知抛物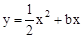线与直线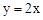交于点O（0，0），。点B是抛物线上O，A之间的一个动点，过点B分别作ｘ轴、ｙ轴的平行线与直线OA交于点C，E。

（1）求抛物线的函数解析式；
（2）若点C为OA的中点，求BC的长；
（3）以BC，BE为边构造条形BCDE，设点D的坐标为（ｍ，ｎ），求ｍ，ｎ之间的关系式。

如图，在平面直角坐标系xOy中，抛物线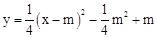的顶点为A，与y轴的交点为B，连结AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连结BD．作AE∥x轴，DE∥y轴．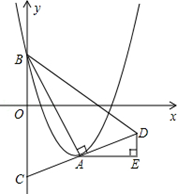

（1）当m=2时，求点B的坐标；
（2）求DE的长？
（3）①设点D的坐标为（x，y），求y关于x的函数关系式？②过点D作AB的平行线，与第（3）①题确定的函数图象的另一个交点为P，当m为何值时，以，A，B，D，P为顶点的四边形是平行四边形？

已知二次函数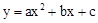（a＞0）的图象与x轴交于A（x₁，0）、B（x₂，0）（x₁＜x₂）两点，与y轴交于点C，x₁，x₂是方程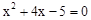的两根．

（1）若抛物线的顶点为D，求S_△ABC：S_△ACD的值；
（2）若∠ADC=90°，求二次函数的解析式．

如图，在等边△ABC中，AB=3，D、E分别是AB、AC上的点，且DE∥BC，将△ADE沿DE翻折，与梯形BCED重叠的部分记作图形L．

（1）求△ABC的面积；
（2）设AD=x，图形L的面积为y，求y关于x的函数解析式；
（3）已知图形L的顶点均在⊙O上，当图形L的面积最大时，求⊙O的面积．

如图，抛物线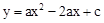（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．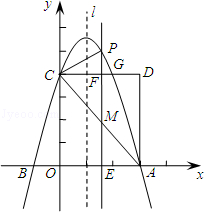

（1）求抛物线的解析式；
（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；
（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由。

先阅读以下材料，然后解答问题：
材料：将二次函数的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式（平移后抛物线的形状不变）。
解：在抛物线上任取两点A（0，3）、B（1，4），由题意知：点A向左平移1个单位得到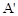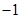（，3），再向下平移2个单位得到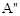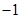（，1）；点B向左平移1个单位得到（0，4），再向下平移2个单位得到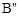（0，2）。
设平移后的抛物线的解析式为。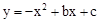
则点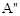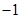（，1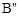），（0，2）在抛物线上。
可得：，解得：。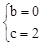
所以平移后的抛物线的解析式为：。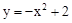
根据以上信息解答下列问题：
将直线向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式。

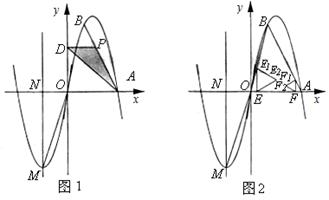
如图1，已知抛物线C经过原点，对称轴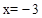与抛物线相交于第三象限的点M，与x轴相交于点N，且。

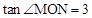（1）求抛物线C的解析式；
（2）将抛物线C绕原点O旋转180⁰得到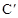抛物线，抛物线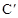与x轴的另一交点为A，B为抛物线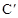上横坐标为2的点。
①若P为线段AB上一动点，PD⊥y轴于点D，求△APD面积的最大值；
②过线段OA上的两点E、F分别作x轴的垂线，交折线O－B－A于E₁、F₁，再分别以线段EE₁、FF₁为边作如图2所示的等边△AE₁E₂、等边△AF₁F2，点E以每秒1个长度单位的速度从点O向点A运动，点F以每秒1个长度单位的速度从点A向点O运动，当△AE₁E₂有一边与△AF₁F₂的某一边在同一直线上时，求时间t的值。