
科目: 来源: 题型:解答题
如图,一次函数y=kx+b的图象与反比例函数y=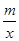 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.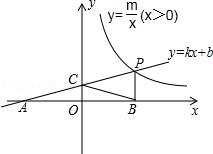
查看答案和解析>>
科目: 来源: 题型:解答题
如图,点A,B分别在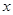 轴,
轴,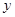 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥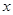 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA=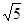 ,反比例函数
,反比例函数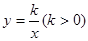 的图象过CD的中点E。
的图象过CD的中点E。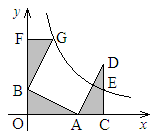
(1)求证:△AOB≌△DCA;
(2)求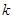 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在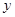 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,经过原点的两条直线 、
、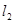 分别与双曲线
分别与双曲线 相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
(1)求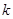 值及
值及 点坐标;(4分)
点坐标;(4分)
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积;(4分)
(3)若P点坐标为(m,n),且 ,求P点坐标.(4分)
,求P点坐标.(4分)
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知函数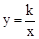 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=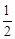 AC时,求CE的长.
AC时,求CE的长.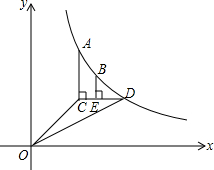
查看答案和解析>>
科目: 来源: 题型:解答题
六•一儿童节,小文到公园游玩,看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等,比如:A、B、C是弯道MN上任三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系(如图).图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米),OG=GH=HI.
(1)求S1和S3的值;
(2)设T 是弯道MN上的任一点,写出y关于x的函数关系式;
是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改选,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?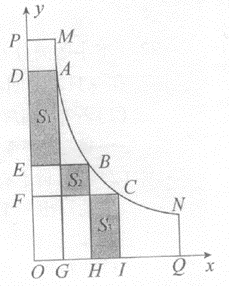
查看答案和解析>>
科目: 来源: 题型:解答题
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数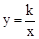 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为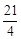 时,求点P的坐标.
时,求点P的坐标.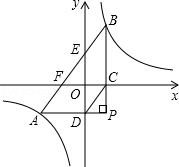
查看答案和解析>>
科目: 来源: 题型:解答题
如图,矩形OABC的顶点B的坐标为(1,2),反比例函数y=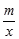 (0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(0<m<2)的图象与AB交于点E,与BC交于点F,连接OE、OF、EF.
(1)若点E是AB的中点,则m= ,S△OEF= ;
(2)若S△OEF=2S△BEF,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得△MFE与△BFE全等?若存在,写出此时点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数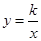 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
⑴求k的值;
⑵若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com