
科目: 来源: 题型:解答题
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).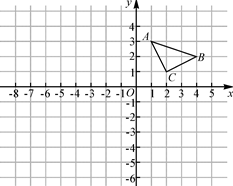
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使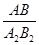 =
=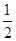 ,并写出点A2的坐标。
,并写出点A2的坐标。
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4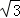 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目: 来源: 题型:解答题
在□ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
在Rt△ABC中,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,
且DM⊥DN,作MF⊥AB于点F,NE⊥AB于点E。
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC。
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明。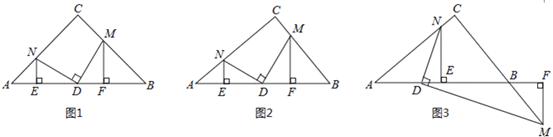
查看答案和解析>>
科目: 来源: 题型:解答题
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E、F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF、AE,AE交BD于点G.
(1)如图l,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM、ED、MF,MF的延长线交ED于点N,∠MBF= ∠BAF,AF=
∠BAF,AF= AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
查看答案和解析>>
科目: 来源: 题型:解答题
数学课上,张老师出示图1和下面的条件:如图1,两个等腰直角三角板ABC和DEF有一条边在同一条直线l上,DE=2,AB=1.将直线EB绕点E逆时针旋转45°,交直线AD于点M.将图1中的三角板ABC沿直线l向右平移,设C、E两点间的距离为k.
解答问题:
(1)①当点C与点F重合时,如图2所示,可得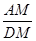 的值为 ;
的值为 ;
②在平移过程中,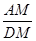 的值为 (用含k的代数式表示);
的值为 (用含k的代数式表示);
(2)将图2中的三角板ABC绕点C逆时针旋转,原题中的其他条件保持不变.当点A落在线段DF上时,如图3所示,请补全图形,计算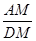 的值;
的值;
(3)将图1中的三角板ABC绕点C逆时针旋转α度,0<α≤90,原题中的其他条件保持不变.计算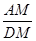 的值(用含k的代数式表示).
的值(用含k的代数式表示).
查看答案和解析>>
科目: 来源: 题型:解答题
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.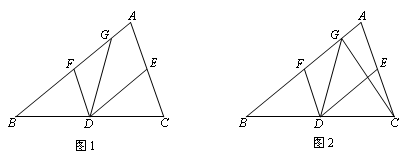
查看答案和解析>>
科目: 来源: 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,tanA= 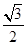 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求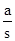 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)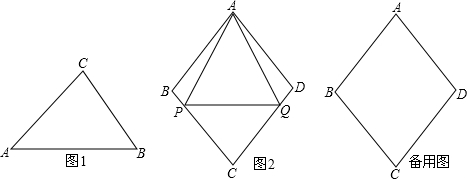
查看答案和解析>>
科目: 来源: 题型:解答题
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.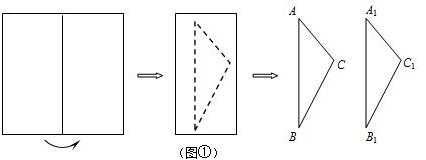
(1)将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.
①求证:四边形C1B1AB为梯形.
②若∠A="45°," ∠ABC="30°," 求∠B1C1C的度数
(2)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(3)在(2)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)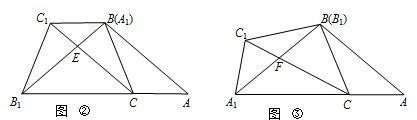
查看答案和解析>>
科目: 来源: 题型:解答题
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC=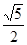 ,DE=2,求AD的长.
,DE=2,求AD的长.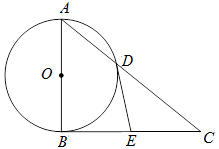
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com