
科目: 来源: 题型:解答题
一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
查看答案和解析>>
科目: 来源: 题型:解答题
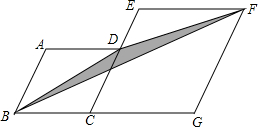
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF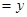 .
.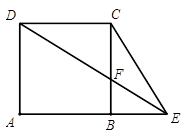
图1
(1)求 关于
关于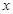 的函数解析式,并写出
的函数解析式,并写出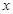 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;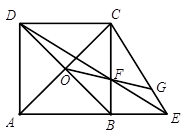
图2
(3)在(2)的条件下,当 时,求
时,求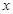 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:解答题
如图:已知一次函数 的图像分别交
的图像分别交 轴、
轴、 轴于
轴于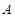 、
、 两点,且点
两点,且点 在一次函数
在一次函数 的图像上,
的图像上,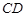 ⊥
⊥ 轴于点
轴于点 .
.
(1)求 的值及
的值及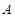 、
、 两点的坐标;
两点的坐标;
(2)如果点 在线段
在线段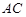 上,且
上,且 ,求
,求 点的坐标;
点的坐标;
(3)如果点 在
在 轴上,那么当△
轴上,那么当△ 与△
与△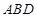 相似时,求点
相似时,求点 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:解答题
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.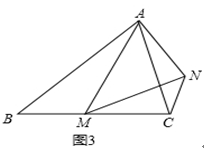
查看答案和解析>>
科目: 来源: 题型:解答题
【探究发现】
按图中方式将大小不同的两个正方形放在一起,分别求出阴影部分(⊿ACF)的面积。(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)
1.S1= cm2; S2= cm2; S3= cm2.
2.归纳总结你的发现: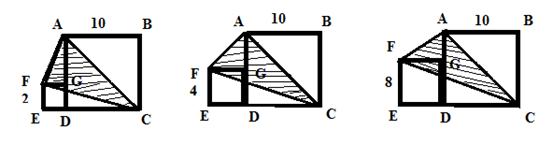
【推理反思】
按图中方式将大小不同的两个正方形放在一起,设小正方形的边长是bcm,大正方形的边长是acm,求:阴影部分(⊿ACF)的面积。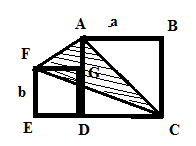
【应用拓展】
1.按上图方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
2.如图(1),C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形⊿ACD和等边三角形⊿CBE,若⊿CBE的边长是1cm,则图中阴影三角形的面积是 cm2.
3.如图(2),菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是 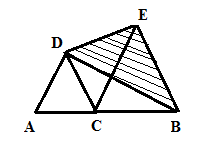
(1) (2)
查看答案和解析>>
科目: 来源: 题型:解答题
如图(1),∆ABC为等边三角形,AB=6,在直角三角板DEF中∠F=90°,∠FDE=60°,点D在边BC上运动,边DF始终经过点A,DE交AC于点G.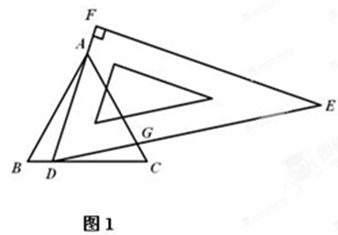
(1)求证:①∠BAD=∠CDG
②∆ABD∽∆DCG
(2)设BD=x,若CG=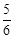 ,求x的值;
,求x的值;
(3)如图2,当D运动到BC中点时,点P为线段AD上一动点,连接CP,将线段CP绕着点C逆时针旋转60°得到CP' ,连接BP',DP',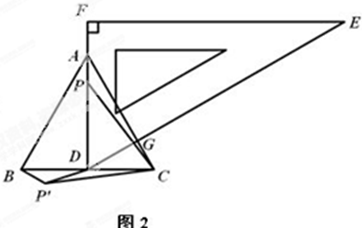
①求∠CBP'的度数;②求DP'的最小值.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135º,得到矩形EFGH(点E与O重合).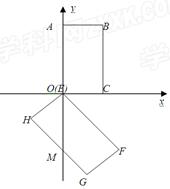
(1)若GH交y轴于点M,则∠FOM= ,OM= .
(2)将矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4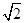 -2时,S与t之间的函数关系式.
-2时,S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
查看答案和解析>>
科目: 来源: 题型:解答题
已知:如图,正方形ABCD的边长为a,BM,DN分别平分正方形的两个外角,且满足 ∠MAN=45°,连结MC,NC,MN.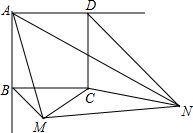
(1)填空:与△ABM相似的三角形是△ ,BM·DN= ;(用含a的代数式表示)
(2)求∠MCN的度数;
(3)猜想线段BM,DN和MN之间的数量关系并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com