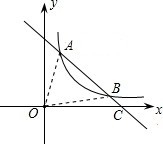如图，双曲线y=

k

x

(x＞0)上有一点A（1，5），过点A的直线y=-mx+n与该双曲线交于点B，且点B的纵坐标为1．
（1）求反比例函数和一次函数的解析式；
（2）连接OA、OB，求△AOB的面积；
（3）根据图象直接写出在第一象限内一次函数的值大于反比例函数的值时，x的取值范围．

先化简，再求值：（

2x-1

x2-4x+4

-

1

x-2

）÷

x+3

x2-4

，其中x满足分式方程

2

x+4

=

1

x

．

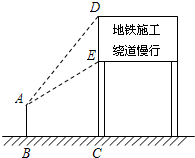某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°．求路况指示牌DE的高度．（精确到0.01米）

在一次羽毛球赛中，甲运动员在离地面

4

3

米的P点处发球，球的运动轨迹PAN看作一个抛物线的一部分，当球运动到最高点A时，其高度为3米，离甲运动员站立地点O的水平距离为5米，球网BC离点O的水平距离为6米，以点O为圆点建立如图所示的坐标系，乙运动员站立地点M的坐标为（m，0）
（1）求抛物线的解析式（不要求写自变量的取值范围）；
（2）求羽毛球落地点N离球网的水平距离（即NC的长）；
（3）乙原地起跳后可接球的最大高度为2.4米，若乙因为接球高度不够而失球，求m的取值范围．

公园中有一棵树和一座塔恰好座落在一条笔直的道路上．在途中A处，小杰测得树顶和塔尖的仰角分别为45°和30°，继续前进8米至B处，又测得树顶和塔尖的仰角分别为16°和45°，试问这棵树和这座塔的高度分别为多少米？（结果精确到0.1米．参考数据：

2

≈1.414，

3

≈1.732，tan16°≈0.287，sin16°≈0.276，cos16°≈0.961）

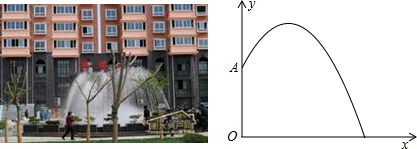
某拱桥的横截面呈抛物线形，桥下水面宽为AB（单位：米）．以水面宽AB所在直线为x轴，以AB垂直平分线为y轴建立如图所示的平面直角坐标系．抛物线解析式为y=-x²+4
（1）水面宽AB是多少？
（2）若点D在抛物线上且D点的横坐标为

1

2

，求△ABD的面积s．

已知：如图，△ABC、直线m、点M在网格中如图所示的位置，请按以下要求作图：
（1）将△ABC向上平移6个单位得△A₁B₁C₁；
（2）作出△ABC关于直线m的轴对称图形△A₂B₂C₂；
（3）作出△A₂B₂C₂绕点M顺时针旋转90°的图形△A₃B₃C₃．

如图，小区中央公园要修建一个圆形的喷水池，在水池中央垂直于地面安装一个柱子OA，O恰好在水面的中心，OA=1.25米．由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计水流在离OA距离为1米处达到距水面的最大高度2.25米．

（1）建立适当的平面直角坐标系，使A点的坐标为（0，1.25），水流的最高点的坐标为（1，2.25），求水流的抛物线路线在第一象限内对应的函数关系式（不要求写取值范围）；
（2）若不计其他因素，则水池的半径至少要多少米，才能使喷出的水流不至于落到池外？
（3）若水流喷出的抛物线形状与（1）相同，水池半径为3.5米，要使水流不落到池外，此时水流距水面的最大高度就达到多少米？

等腰三角形ABC的面积为10，AB=AC=5，那么BC= 或．

甲，乙两个形状完全相同的容器都装有大小分别相同的一个进水管和一个出水管，两容器单位时间进、出的水量各自都是一定的．已知甲容器单开进水管第10分钟把空容器注满；然后同时打开进、出水管，第30分钟可把甲容器的水放完，甲容器中的水量Q（升）随时间t（分）变化的图象如图1所示．而乙容器内原有一部分水，先打开进水管5分钟，再打开出水管，进、出水管同时开放，第20分钟把容器中的水放完，乙容器中的水量Q（升）随时间t（分）变化的图象如图2所示，则乙容器内原有水升．