计算：sin45°－tan60°·cos30°．

如图，点D是△ABC的边AC上的一点，AB2＝AC·AD．求证：△ADB∽△ABC．

如图，正比例函数y=2x与反比例函数的图象的一个交点为A（2，m）．

求m和k的值．

如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，点A，B，C的坐标分别为（0，1），（1，－1），（5，1）．

（1）直接写出点B关于原点的对称点D的坐标；

（2）将△ABC绕点C顺时针旋转90º得到△A1B1C．请在网格中画出△A1B1C，并直接写出点A1和B1的坐标．

如图，在半径为6cm的⊙O中，圆心O到弦AB的距离OE为3cm．

（1）求弦AB的长；（2）求劣弧的长．

在燕房线地铁施工期间，交管部门在施工路段设立了矩形路况警示牌（如图所示）．已知立杆AB的高度是3米，从路侧点D处测得路况警示牌顶端C点和底端B点的仰角分别是60°和45°，求路况警示牌宽BC的值．（精确到0.1米）（参考数据：≈1.41，≈1.73）

如图，四边形ABCD的对角线AC，BD交于点F，点E是BD上一点，且∠BAC＝∠BDC＝∠DAE．

（1）求证：△ABE∽△ACD；

（2）若BC＝2，AD＝6，DE＝3，求AC的长．

根据某网站调查，2014年网民们最关注的热点话题分别有：消费、教育、环保、反腐及其它共五类．根据调查的部分相关数据，绘制的统计图表如下

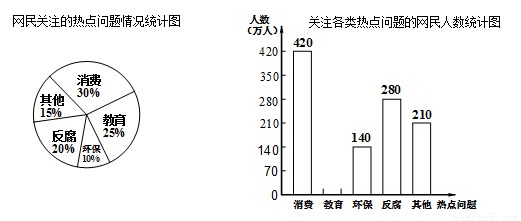
根据以上信息解答下列问题：

（1）请补全条形统计图并在图中标明相应数据；

（2）若北京市约有2100万人口，请你估计最关注环保问题的人数约为多少万人？

（3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，则抽取的两人恰好是甲和乙的概率为 ．

如图，AB为⊙O的直径，直线与⊙O相切于点C，过点A作AD⊥于点D，交⊙O于点E．

（1）求证：∠CAD＝∠BAC；[（2）若sin∠BAC＝，BC＝6，求DE的长．

阅读下面材料：

小辉遇到这样一个问题：如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D，E在边BC上，∠DAE＝45°．若BD＝3，CE＝1，求DE的长．

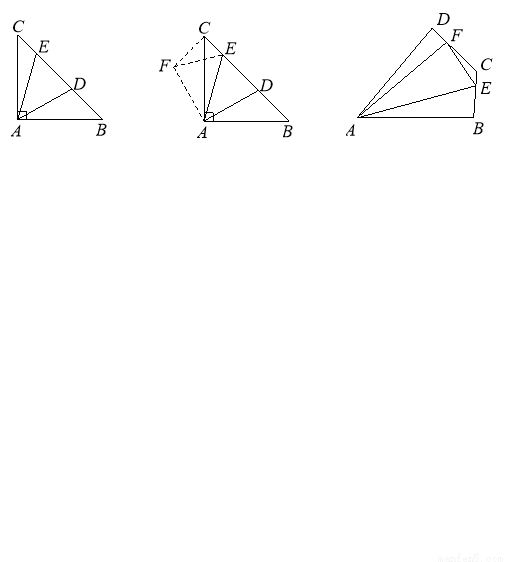
小辉发现，将△ABD绕点A按逆时针方向旋转90º，得到△ACF，连接EF（如图2），由图形旋转的性质和等腰直角三角形的性质以及∠DAE＝45°，可证△FAE≌△DAE，得FE＝DE．解△FCE，可求得FE（即DE）的长．

请回答：在图2中，∠FCE的度数是 ，DE的长为 ．

参考小辉思考问题的方法，解决问题：

如图3，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°．E，F分别是边BC，CD上的点，且∠EAF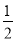＝∠BAD．猜想线段BE，EF，FD之间的数量关系并说明理由．