
科目: 来源: 题型:
有一辆汽车在中途受阻,耽 误了6分钟,然后将速度由原来的每小时40千米,提高到每小时50千米,若要将耽误的时间补上,则需这样走( ).
误了6分钟,然后将速度由原来的每小时40千米,提高到每小时50千米,若要将耽误的时间补上,则需这样走( ).
A.10千米 B.20千米
C.40千米 D.50千米
查看答案和解析>>
科目: 来源: 题型:
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
(1)请你直接写出“蛋圆”抛物线部分的解析式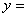 ,自变量的取值范围是 ;
,自变量的取值范围是 ;
(2)请你求出过点C的“蛋圆”切线与x轴的 交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.


查看答案和解析>>
科目: 来源: 题型:
(1)在Rt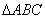 中,∠C = 90°, ∠B = 30°.
中,∠C = 90°, ∠B = 30°.
①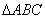 绕点C顺时针旋转得到
绕点C顺时针旋转得到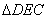 ,点
,点 恰好落在
恰好落在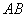 边上.如图1,则
边上.如图1,则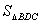 与
与 的数量关系是 ;
的数量关系是 ;
②当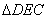 绕点C旋转到图2的位置时,小娜猜想①中
绕点C旋转到图2的位置时,小娜猜想①中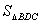 与
与 的数量关系仍然成立,并尝试分别作出了
的数量关系仍然成立,并尝试分别作出了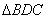 和
和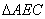 中BC,C
中BC,C 边上的高,请你证明小娜的猜想;[来源:学_科_网]
边上的高,请你证明小娜的猜想;[来源:学_科_网]
(2)已知,∠ABC = 60°,点 是∠ABC平分线上一点,
是∠ABC平分线上一点,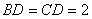 ,
, 交
交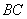 于点
于点 ,如图3.若在射线
,如图3.若在射线 上存在点
上存在点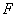 ,使
,使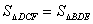 ,则
,则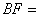
 .
.



1 图2  图3
图3
查看答案和解析>>
科目: 来源: 题型:
已知抛物线 与
与 轴相交于
轴相交于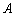 ,
,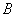 两点(点
两点(点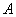 在点
在点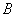 的左侧),与
的左侧),与
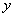 轴相交于点
轴相交于点 .
.
(1)点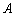 的坐标为 ,点
的坐标为 ,点 的坐标为 ;
的坐标为 ;
(2)在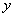 轴的正半轴上是否存在点
轴的正半轴上是否存在点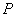 ,使以点
,使以点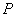 ,
,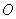 ,
,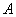 为顶点的三角形与
为顶点的三角形与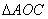 相似?若存在,求出点
相似?若存在,求出点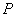 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是矩形,且DE⊥CF.
则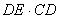
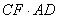 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);
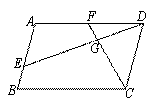
(2)如图2,若四边形ABCD是平行四边形,试探究:
当∠B与∠EGC满足什么关系时,使得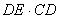 =
=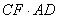
成立?并证明你的结论;
(3)如图3,若BA=BC= 3,DA=DC= 4,∠BAD= 90°,DE⊥CF.则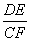 的值为
的值为
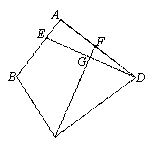
 .
.

图1 图2 图3
查看答案和解析>>
科目: 来源: 题型:
在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x (元)的一次函数.
(1)直接写出y与x之间的函数关系式y = .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目: 来源: 题型:
如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
(1)点D在线段PQ上,且DQ=DC.
求证:CD是⊙O的切线;
(2)若sinQ= ,BP =6,AP =
,BP =6,AP = ,求QC的长.
,求QC的长.

查看答案和解析>>
科目: 来源: 题型:
已知二次函数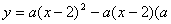 为常数,且
为常数,且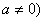 .
.
(1)求证:不论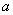 为何值,该函数的图象与
为何值,该函数的图象与 轴总有两个公共点;
轴总有两个公共点;
(2)设该函数的图象的顶点为C,与 轴交于A,B两点,当△ABC
轴交于A,B两点,当△ABC
的面积等于2时,求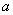 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com