如果,那么,两个实数一定是(   ) 

A. 互为倒数       B.-1和+1       C.互为相反数      D.互为负倒数

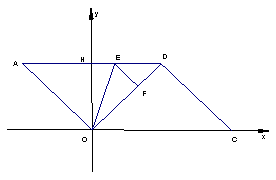
如图，在直角坐标系中，平行四边形AOCD的边OC在x轴上，边AD与y轴交与点H，CD=10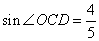，。点E、F分别是边AD和对角线OD上的动点（点E不与A、D重合），

∠OEF=∠A=∠DOC，设AE=t,OF=s。

(1) 求直线DC的解析式；

(2) 求s关于t的函数关系式，并写出t的取值范围；

(3) 点E在边AD上移动的过程中，△OEF是否有可能成为一个等腰三角形？若有可能，请求出t的值，若不可能，请说明理由。

如图，两个同心圆的圆心是O，大圆的半径为10，小圆的半径为6，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．

(1)求BD 的长；

(2)求∠ABE+2∠D的度数；

(3)求的值．（改编）

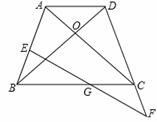
如图，在四边形ABCD中，AD＜BC，对角线AC、BD相交于O点，AC=BD，∠ACB=∠DBC.

（1）求证：四边形ABCD为等腰梯形.

（2）若E为AB上一点，延长DC至F，使CF=BE，连接EF  交BC于G，请判断G点是否为EF中点，并说明理由.

如图，某学习小组为了测量河对岸塔AB的高度，在塔底部B的正对岸点C处测得塔顶仰角∠ACB=30°

（1）若河宽BC是60米，求塔AB的高（精确到0.1米；参考数据）

（2）若河宽BC无法度量．则应如何测量塔AB的高度呢？小明想出了另外一种方法：从点C出发，沿河岸CD的方向（点B、C、D在同一平面内，且CD⊥BC）走a米到达D处，测得∠BDC=60°，这样就可以求得塔AB的高度了．请你用这种方法求出塔AB的高。

、、

将背面完全相同，正面上分别写有数字1、2、3、4的四张卡片混合后，小明从中随机地抽取一张，把卡片上的数字作为被减数；再将形状、大小完全相同，分别标有数字1、2、3的三个小球混合后，小华从中随机地抽取一个，把小球上的数字作为减数，然后计算出这两个数的差.

（1）请你用画树状图或列表的方法，求这两数差为0的概率.

（2）小明与小华做游戏，规则是：若这两数的差为非负数，则小明赢；否则，小华赢.你认为该游戏公平吗？请说明理由.如果不公平，请你修改游戏规则，使游戏公平. （习题改编）

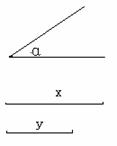
（1）已知∠α和线段x,y（如图）。用直尺和圆规作出△ABC，

使∠A＝∠α，AB＝x，BC＝y

(要求画出图形，并保留作图痕迹，不必写出作法)

（2）已知两边及其中一边的对角，你能作出满足这样条件的三角吗？  有几种可能？（习题改编）

化简：a（b+1）﹣ab﹣1．

计算：

在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作，如图所示．若AB=4，AC=2，S₁﹣S₂=，则S₃﹣S₄的值是