
科目: 来源: 题型:
在平面直角坐标系xOy中,已知二次函数y1=ax2+3x+c的图像经过原点及点
A(1,2), 与x轴相交于另一点B.
(1)求:二次函数y1的解析式及B点坐标;
(2)若将抛物线y1以x=3为对称轴向右翻折后,得到一个新的二次函数y2,已知二次函数y2与x轴交于两点,其中右边的交点为C点. 点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);
①当点E在二次函数y1的图像上时,求OP的长.
②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,同时线段OC上另一个点Q从C点出发向O点做匀速运动,速度为每秒2个单位长度(当Q点到达O点时停止运动,P点也同时停止运动).过Q点作x轴的垂线,与直线AC交于G点,以QG为边在QG的左侧作正方形QGMN(当Q点运动时,点G、点M、点N也随之运动),若P点运动t秒时,两个正方形分别有一条边恰好落在同一条直线上(正方形在x轴上的边除外),求此刻t的值.
查看答案和解析>>
科目: 来源: 题型:
如图,已知△ABC的三个顶点坐标分别为A(-4,0). B(1, 0). C(-2, 6).
(1)求经过点A. B. C三点的抛物线解析式。
(2)设直线BC交y轴于点E,连结AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连结AD交BC于点F,求证:以A. B. F为顶点的三角形与△ABC相似,并求: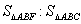 。
。
查看答案和解析>>
科目: 来源: 题型:
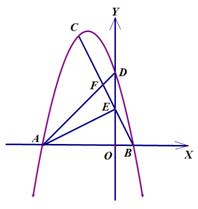
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度)
(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
查看答案和解析>>
科目: 来源: 题型:
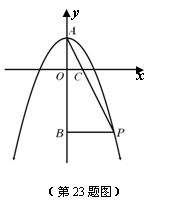
如图,抛物线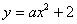 与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C, ,且S△AOC=1,过点P作PB⊥y轴于点B.
,且S△AOC=1,过点P作PB⊥y轴于点B.
(1)求BP的长;
(2)求抛物线与x轴的交点坐标.
 |
查看答案和解析>>
科目: 来源: 题型:
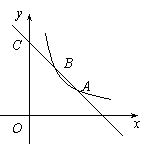
如图,函数y1=k1x+b的图象与函数y2=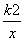 (x>0)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(x>0)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数y1的表达式和点B的坐标;
(2)观察图象,比较当x>0时y1与y2的大小.
查看答案和解析>>
科目: 来源: 题型:
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
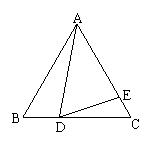 |
查看答案和解析>>
科目: 来源: 题型:
已知二次函数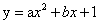 的图像过点(1,0)和(
的图像过点(1,0)和( ),且-2<
),且-2<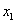 <-1,现在有5个判断:
<-1,现在有5个判断:
b<0 (2)b-a<0 (3)a>b-1 (4)a< (5)2a<b+
(5)2a<b+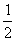 ,请把你认为判断正确的序号写出来 。
,请把你认为判断正确的序号写出来 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com