
科目: 来源: 题型:
阅读材料:
对于平面内的任意两点A(x1,y1),B(x2,y2),
由勾股定理易知A、B两点间的距离公式为:
AB=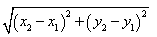 .
.
如:已知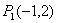 ,
,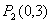 ,
,
则
解答下列问题:
已知点E(6,10),F(0,2),C(0,1)。
(1)直接应用平面内两点间距离公式计算,
E、F之间的距离为_ _5及代数式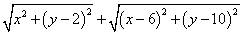 的最小值为 ;
的最小值为 ;
(2)求以C为顶点,且经过点E的抛物线的解析式;
(3)①若点D是上述抛物线上的点,且其横坐标为 -3,试求DF的长;
②若点P是该抛物线上的任意一点,试探究线段FP的长度与点P纵坐标的数量关系,并证明你的猜想。
③我们知道“圆可以看成是所有到定点的距离等于定长的点的集合”。类似地,抛物线可以看成是_______________________________________.
 |
查看答案和解析>>
科目: 来源: 题型:
如图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.
思考:如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α。
当α=__ __度时,点P到CD的距离最小,最小值为__  __.
__.
探究一:在图1的基础上,以点M为旋转中心,在AB,CD 之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO=_ __度,此时点N到C D的距离是__ __.
D的距离是__ __.
探究二:将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。
(1)如图3,当α=60°时,求 在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请直接确定α的最大值=__ __.

查看答案和解析>>
科目: 来源: 题型:
某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要 求写自变量的取值范围)
求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源: 题型:
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)请完成如下操作:①建立平面直角坐标系,使得B点坐标为(4,4); ②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连结AD、CD.
(2)请在(1)的基础上,完成下列问题:
① 写出点的坐标:C______ __、D_____ ___;
② ⊙D的半径=_________(结果保留根号);
③ 若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面面积=______ _____(结果保留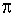 ).
).
查看答案和解析>>
科目: 来源: 题型:
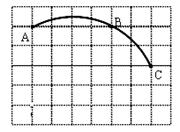
如图所示,将一个可以自由转动的转盘分成三等分,每一份内标上数字,第一次转动转盘,当转盘停止后,指针所在的区域的数字记为a,第二次转动转盘,当转盘停止后,指针所在的区域的数字记为b(注意:如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)求得抛物线y= ax2+bx+2开口向下的概率为____;
ax2+bx+2开口向下的概率为____;
(2)用画树状图或列表格的方法,求抛物线y=ax2+bx+2的对称轴在y轴左侧的概率.
查看答案和解析>>
科目: 来源: 题型:
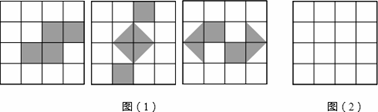
如图所示,网格中每个小正方形的边长为1,请你认真观察图(1)中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:
①都是___对称图形;②阴影部分面积都是___;③都不是___对称图形.
(2)请你在图(2)中设计出一个具备上述特征的图案(图中已给出除外).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com