
科目: 来源: 题型:
某校七(2)班42名同学为“希望工程”捐款,共捐款320元,捐款情况如下表:
| 捐款(元) | 4 |
| 8 | 10 | ||
| 人 数 | 6 | 7 |
表格中捐款6元和8元的人数不小心被墨水污染已看不清楚.若设捐款6元的
有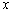 名同学,捐款8元的有
名同学,捐款8元的有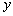 名同学,根据题意,可得方程组( )
名同学,根据题意,可得方程组( )
A.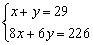 B.
B.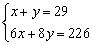 C.
C.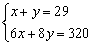 D.
D.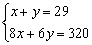
查看答案和解析>>
科目: 来源: 题型:
下列从左到右的变形属于因式分解的是( )
A.x2 –2xy+y2=x(x-2y)+y2 B.x2-16y2=(x+8y)(x-8y)
C.x2+xy+y2=(x+y)2 D. x4y4-1=(x2y2+1)(xy+1)(xy-1)
查看答案和解析>>
科目: 来源: 题型:
下列每组数据表示3根小木棒的长度,其中能组成一个三角形的是( )
A.3cm,4cm,7cm B.3cm,4cm,6cm
C.5cm,4cm,10cm D.5cm,3cm,8cm
查看答案和解析>>
科目: 来源: 题型:
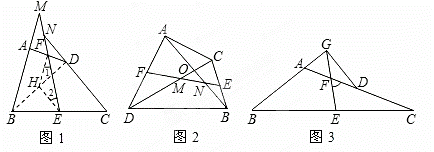
如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并 延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H, 连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,并说明理由;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分 别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,
别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G, 若∠EFC=60°,连接GD,判断△AGD的形状并并说明理由.
若∠EFC=60°,连接GD,判断△AGD的形状并并说明理由.
查看答案和解析>>
科目: 来源: 题型:
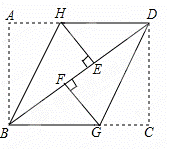
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com