
科目: 来源: 题型:
(2014年黑龙江哈尔滨)哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A. 5℃ B. 6℃ C. 7℃ D. 8℃
查看答案和解析>>
科目: 来源: 题型:
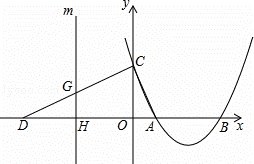
如图,抛物线y=ax2﹣8ax+12a(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(1)请直接写出A、B两点的坐标;
(2)求抛物线的解析式;
(3)抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标及周长的最小值;若不存在,说明理由;
(4)平行于y轴的直线m从点D出发沿x轴向右平行移动,到点A停止.设直线m与折线DCA的交点为G,与x轴的交点为H(t,0).记△ACD在直线m左侧部分的面积为s,求s关于t的函数关系式及自变量t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
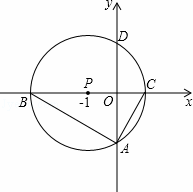
如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2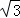 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
|
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
查看答案和解析>>
科目: 来源: 题型:
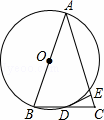
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若AB=13,sinB=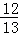 ,求CE的长.
,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
在一个不透明的口袋里装有分别标有数字﹣3、﹣1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标记为x(不放回);在任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
查看答案和解析>>
科目: 来源: 题型:
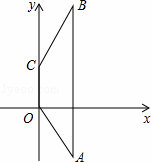
如图,在梯形OABC中,OC∥AB,OA=CB,点O为坐标原点,且A(2,﹣3),C(0,2).
(1)求过点B的双曲线的解析式;
(2)若将等腰梯形OABC向右平移5个单位,问平移后的点C是否落在(1)中的双曲线上?并简述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com