
科目: 来源: 题型:
在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的早间新闻.据此,估计该镇看中央电视台早间新闻的约有( )
|
| A. | 2.5万人 | B. | 2万人 | C. | 1.5万人 | D. | 1万人 |
查看答案和解析>>
科目: 来源: 题型:
据统计,我国2013年全年完成造林面积约6090000公顷.6090000用科学记数法可表示为( )
|
| A. | 6.09×106 | B. | 6.09×104 | C. | 609×104 | D. | 60.9×105 |
查看答案和解析>>
科目: 来源: 题型:
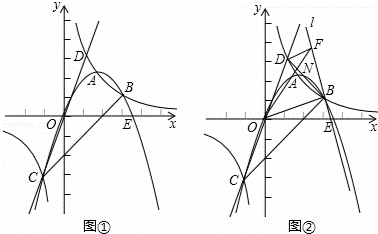
如图①,双曲线y=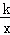 (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求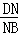 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
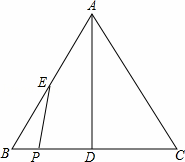
如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,P是BC边上的动点(不与B,C重合).设BP=x.
(1)当x=6时,求PE的长;
(2)当△BPE是等腰三角形时,求x的值;
(3)当AD平分EP时,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
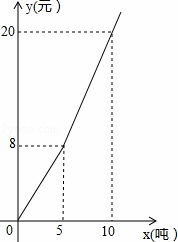
随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按 元收取;超过5吨的部分,每吨按 元收取;
(2)请写出y与x的函数关系式;
(3)若某个家庭有5人,五月份的生活用水费共76元,则该家庭这个月人均用了多少吨生活用水?
查看答案和解析>>
科目: 来源: 题型:
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
(1)若四边形ABCD是菱形,则它的中点四边形EFGH一定是 ;
A.菱形 B.矩形 C.正方形 D.梯形
(2)若四边形ABCD的面积为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是S1= S2
(3)在四边形ABCD中,沿中点四边形EFGH的其中三边剪开,可得三个小三角形,将这三个小三角形与原图中未剪开的小三角形拼接成一个平行四边形,请在答题卡的图形上画出一种拼接示意图,并写出对应全等的三角形.

查看答案和解析>>
科目: 来源: 题型:
某校九年级有10个班,每班50名学生,为调查该校九年级学生一学期课外书籍的阅读情况,准备抽取50名学生作为一个样本惊醒分析,并规定如下:设一个学生一学期阅读课外书籍本书为n,当0≤n<5时为一般读者;当5≤n<10时为良好读者;当n≥10时为优秀读者.
(1)下列四种抽取方法最具有代表性的是 B ;
A.随机抽取一个班的学生 B.随机抽取50名学生
C.随机抽取50名男生 D.随机抽取50名女生
(2)由上述最具代表性的抽取方法抽取50名学生一学期阅读本数的数据如下:
8 10 6 9 7 16 8 11 0 13 10 5 8
2 6 9 7 5 7 6 4 12 10 11 6 8
14 15 7 12 13 8 9 7 10 12 11 8 13
10 4 6 8 13 6 5 7 11 12 9
根据以上数据回答下列问题
①求样本中优秀读者的频率;
②估计该校九年级优秀读者的人数;
③在样本为一般读者的学生中随机抽取2人,用树形图或列表法求抽得2人的课外书籍阅读本数都为4的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com