
科目: 来源: 题型:
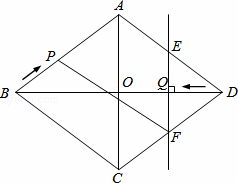
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
数学问题:计算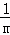 +
+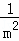 +
+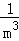 +…+
+…+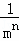 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
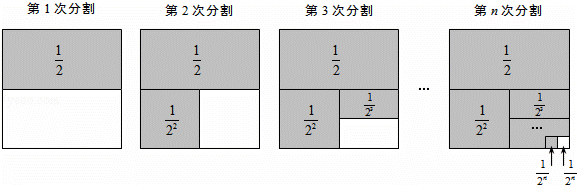
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算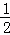 +
+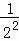 +
+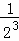 +…+
+…+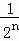 .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为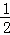 ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为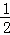 +
+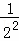 ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为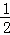 +
+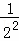 +
+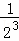 +…+
+…+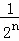 ,最后空白部分的面积是
,最后空白部分的面积是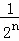 .
.
根据第n次分割图可得等式: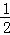 +
+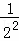 +
+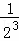 +…+
+…+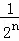 =1﹣
=1﹣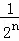 .
.
探究二:计算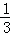 +
+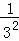 +
+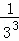 +…+
+…+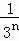 .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为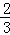 ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为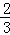 +
+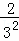 ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为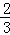 +
+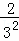 +
+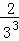 +…+
+…+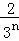 ,最后空白部分的面积是
,最后空白部分的面积是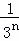 .
.
根据第n次分割图可得等式: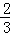 +
+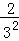 +
+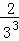 +…+
+…+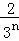 =1﹣
=1﹣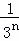 ,
,
两边同除以2,得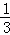 +
+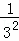 +
+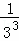 +…+
+…+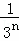 =
=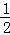 ﹣
﹣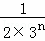 .
.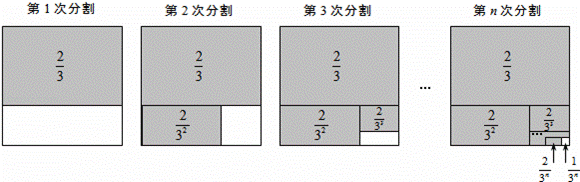
探究三:计算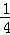 +
+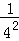 +
+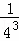 +…+
+…+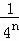 .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算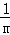 +
+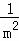 +
+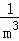 +…+
+…+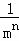 .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式: 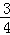 +
+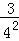 +
+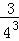 +…+
+…+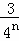 =1﹣
=1﹣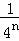 ,
,
所以,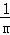 +
+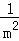 +
+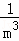 +…+
+…+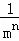 =
= 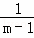 ﹣
﹣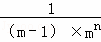 .
.
拓广应用:计算 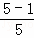 +
+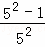 +
+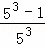 +…+
+…+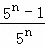 .
.
查看答案和解析>>
科目: 来源: 题型:
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目: 来源: 题型:
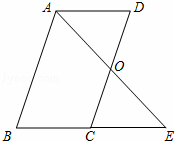
已知:如图,▱ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
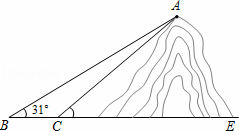
如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈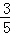 ,sin31°≈
,sin31°≈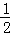 ,tan39°≈
,tan39°≈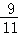 ,sin39°≈
,sin39°≈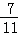 )
)
查看答案和解析>>
科目: 来源: 题型:
甲、乙两人进行赛跑,甲比乙跑得快,现在甲让乙先跑10米,甲再起跑.图中l1和l2分别表示甲、乙两人跑步的路程y(m)与甲跑步的时间x(s)之间的函数关系,其中l1的关系式为y1=8x,问甲追上乙用了多长时间?
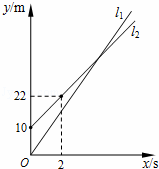
查看答案和解析>>
科目: 来源: 题型:
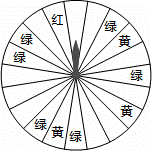
某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目: 来源: 题型:
空气质量状况已引起全社会的广泛关注,某市统计了2013年每月空气质量达到良好以上的天数,整理后制成如下折线统计图和扇形统计图.

根据以上信息解答下列问题:
(1)该市2013年每月空气质量达到良好以上天数的中位数是 天,众数是 天;
(2)求扇形统计图中扇形A的圆心角的度数;
(3)根据以上统计图提供的信息,请你简要分析该市的空气质量状况(字数不超过30字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com