
科目: 来源: 题型:
去年我市参加中考人数约17700人,这个数用科学记数法表示是( )
|
| A. | 1.77×102 | B. | 1.77×104 | C. | 17.7×103 | D. | 1.77×105 |
查看答案和解析>>
科目: 来源: 题型:
已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1,y1),B(x2,y2).
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1,y1),B(x2,y2).
(1)求该二次函数的解析式.
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
(注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的 比的相反数,两根的积等于常数项与二次项系数的比.
比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1,x2,
则:x1+x2=﹣ ,x1•x2=
,x1•x2=
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ,x1•x2=
,x1•x2=
∴原方程两根之和=﹣ =3,两根之积=
=3,两根之积= =﹣15.
=﹣15.

查看答案和解析>>
科目: 来源: 题型:
如图,正方形ABCD的边长为l,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.

查看答案和解析>>
科目: 来源: 题型:
如图,函数y=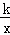 的图象过点A(1,2).
的图象过点A(1,2).
(1) 求该函数的解析式;
求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.

查看答案和解析>>
科目: 来源: 题型:
一位射击运动员在10次射击训练中,命中靶的环数如图.
请你根据图表,完成下列问题:
(1)补充完成下面成绩表单的填写:
| 射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com