
科目: 来源: 题型:
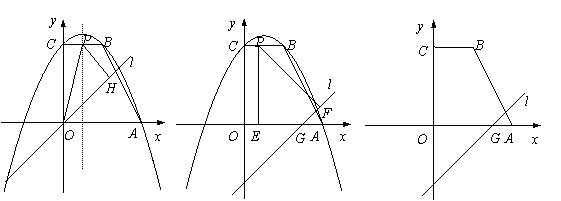
如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式.
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.
 ②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
|
查看答案和解析>>
科目: 来源: 题型:
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F, 连结AF,BE相交于点P.
(1)若AE=CF.
①求证:AF=BE,并求∠APB的度数.
②若AE=2,试求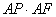 的值.
的值.
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.

查看答案和解析>>
科目: 来源: 题型:
 |
(1)阅读合作学习内容,请解答其中的问题.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,义乌市某服装厂每件衣服原材料的成本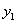 (元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本 (元)与月份x的函数关系式为
(元)与月份x的函数关系式为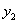 =x+62(8≤x≤12,且x为整数).
=x+62(8≤x≤12,且x为整数).
(1) 请观察表格中的数据,用学过的函数相关知识求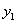 与x的函数关系式.
与x的函数关系式.
(2) 若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量 (万件)与月份x满足关系式
(万件)与月份x满足关系式 =0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量
=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量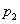 (万件)与月份x满足关系式
(万件)与月份x满足关系式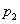 =
= -0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
-0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
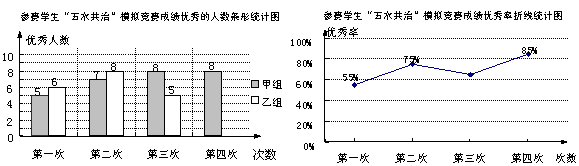
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整.
(2)已求得甲组成绩优秀人数的平均数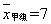 ,方差
,方差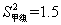 ,请通过计算说明,哪一组成绩优秀的人数较稳定?
,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com