
科目: 来源: 题型:
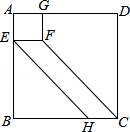
如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 3 |
查看答案和解析>>
科目: 来源: 题型:
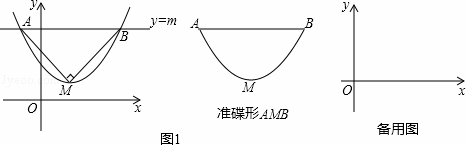
如图1,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟高.
(1)抛物线y=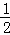 x2对应的碟宽
x2对应的碟宽 为 4 ;抛物线y=4x2对应的碟宽为
为 4 ;抛物线y=4x2对应的碟宽为 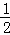 ;抛物线y=ax2(a>0)对应的碟宽为
;抛物线y=ax2(a>0)对应的碟宽为  ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为
;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为  ;
;
(2)抛物线y=ax2﹣4ax﹣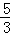 (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
(3)将抛物线y=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3…),定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为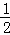 ,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn,则hn= ,Fn的碟宽有端点横坐标为 ;F1,F2,…,Fn的碟宽右端点是否在一条直线上?若是,直接写出该直线的表达式;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
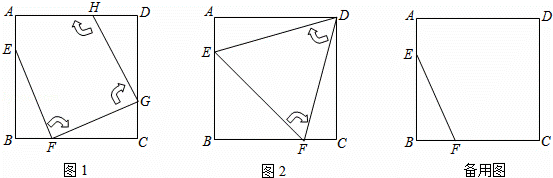
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 等边三角形 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 正方形 ,此时AE与BF的数量关系是 AE=BF ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
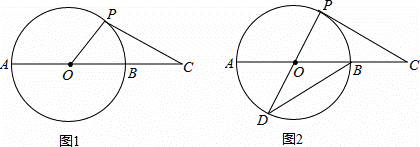
查看答案和解析>>
科目: 来源: 题型:
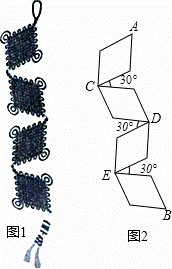
图1中的中国结挂件是由四个相同的菱形在顶点处依 次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
(1)连接CD,EB,猜想它们的位置关系并加以证明;
(2)求A,B两点之间的距离(结果取整数,可以使用计算器)
(参考数据: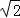 ≈1.41,
≈1.41,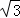 ≈1.73,
≈1.73,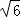 ≈2.45)
≈2.45)
查看答案和解析>>
科目: 来源: 题型:
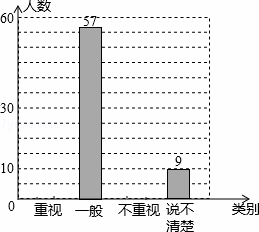
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com