
科目: 来源: 题型:
若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2, 3),则另一个交点的坐标是( )
A、(2, 3) B、(3, 2) C、( , 3) D、(
, 3) D、( ,
,  )
)
查看答案和解析>>
科目: 来源: 题型:
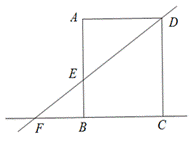
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6.
(1)若点P是边AD上的一个动点(不与点A、D重合),PH⊥DE于H,设DP为x,四边形AEHP的面积为y,试求y与x的函数解析式;
(2)若AE=2EB.
①求圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长;
②半径为4,圆心在直线DF上,且与矩形ABCD的至少一边所在直线相切的圆共有多少个?(直接写出满足条件的圆的个数即可.)
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
(1)当k=-2时,求反比例函数的解析式;
(2)已知经过原点O的两条直线AB与CD分别与双曲线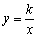 (k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
(k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
问:平行四边形ABCD能否成为矩形?能否成为正方形?若能,请说明直线AB、CD的位置关系;若不能,请说明理由
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
查看答案和解析>>
科目: 来源: 题型:
)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的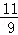 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,抛物线y=mx2﹣2mx﹣2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(3)若该抛物线在2<x<3这一段位于直线AB的下方,
并且在3<x<4这一段位于直线AB的上方,求该抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
一农妇在市场卖葱,当时市场上的葱价是1.00元一斤,一葱贩对农妇说:“我想把你的葱分开来买,葱叶0.50元一斤,葱白0.50元一斤.”农妇听了葱贩的话,不假思索就把葱全部卖完.当农妇数过钱之后才发现只卖了一半钱。此时葱贩已不见踪影.聪明的你,请运用数学语言揭穿葱贩的把戏.
过程如下:设总量z斤,葱叶x斤,葱白y斤,列方程
∵x+y=z,∴卖给葱贩的钱为0.5x+0.5y=0.5z,
而实际应卖的钱为1.0x+1.0y=1.0z,结果一目了然,那葱贩只用了一半钱就买了所有葱.
生活常识告诉我们,人们在吃葱的时候主要吃的是葱白,葱白应比葱叶卖的贵.
假设一根葱的葱叶和葱白重量相同,葱叶和葱白的价钱之和仍是1.00元.请用数学语言说明此时农妇还是只卖了一半的钱.
假设一根葱的葱叶和葱白重量不同,且葱叶的重量大于葱白的重量,葱叶0.20元一斤,葱白0.80元一斤.请用数学语言说明此时农妇卖的钱少于一半.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com