PM3.5是大气中直径小于或等于0.0000035米的颗粒物，将0.0000035用科学记数法表示为（）

A .      B.     C .    D .

（1）探究新知：

①如图，已知AD∥BC，AD＝BC，点M，N是直线CD上任意两点．求证：△ABM与△ABN的面积相等． 

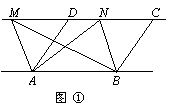
②如图，已知AD∥BE，AD＝BE，AB∥CD∥EF，点M是直线CD上任一点，点G是直线EF上任一点．试判断△ABM与△ABG的面积是否相等，并说明理由．  

（2）结论应用：    

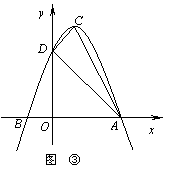
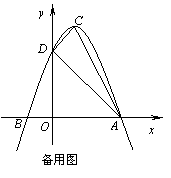
如图③，抛物线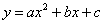的顶点为C（1，4），交x轴于点A（3，0），交y轴于点D．试探究在抛物线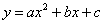上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？ 若存在，请求出此时点E的坐标，若不存在，请说明理由．【改编】    

某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．

（1）当MN和AB之间的距离为0.5米时，求此时△EMN的面积；

（2）设MN与AB之间的距离为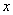米，试将△EMN的面积S（平方米）表示成关于x的函数； 

（3）请你探究△EMN的面积S（平方米）有无最大值，若有，请求出这个最大值；若没有，请说明理由．

已知：关于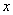的一元二次方程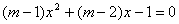（m为实数）

（1）若方程有两个不相等的实数根，求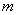的取值范围；

（2）在（1）的条件下，求证：无论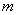取何值，抛物线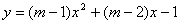总过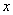轴上的一个固定点；

（3）若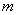是整数，且关于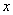的一元二次方程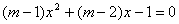有两个不相等的整数根，把抛物线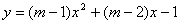向右平移3个单位长度，求平移后的解析式．

某旅游区的游览路线图如图所示．小明通过入口后，每逢路口都任选一条道．

（1）问他进入A景区或B景区的可能性哪个较大?请说明理由。（利用树状图或列表来求解）

（2）如果左边的两条道路变成一条，还可以比较可能性大小吗？请说明你的理由.

（3）通过对（1）（2）的研究，请看古老的谜题Nim游戏

规则一.有三堆石子分别有3颗、4颗、5颗，游戏双方轮流拿石子；规则二.每人每次只能从其中的一堆取，最少要取一颗，最多可以全部取走，可以任意选择；规则三.规定其中一方先拿，拿到最后一颗者赢.问这个游戏机会均等吗？直接写出答案即可.             

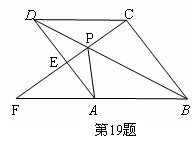
如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．试问：

(1) 图中△APD与哪个三角形全等？并说明理由．

    (2) 猜想：线段PC、PE、PF之间存在什么关系？并说明理由．

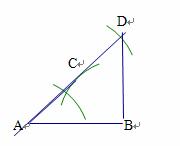
在一次研究性学习活动中，同学们发现了一种直角三角形的作法，方法是(如图所示)：画线段AB，分别以点A、B为圆心，以大于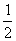AB的长为半径画弧，两弧相交于点C，连结AC；再以点C为圆心，以AC长为半径画弧，交AC的延长线于D，连结DB.则△ABD就是直角三角形.

（1）请证明此作法的正确性；

（2）请利用上述方法作一个直角三角形，使其一个锐角为30°(写出作法，保留作图痕迹).

有下面3个结论: ① 存在两个不同的无理数, 它们的积是整数； ② 存在两个不同的无理数, 它们的差是整数； ③ 存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数.

已知正方形ABCD的边长为5，E在BC边上运动，DE的中点G绕，EG绕E顺时间旋转90°得EF，问CE=           时，A、C、F在一条直线上。

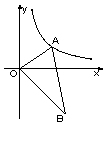
Rt△AOB中，O为坐标原点，∠AOB=90°，∠B=30°，如果点A在反比例函数y=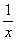（x>0）的图像上运动，那么点B在函数                  （填函数解析式，x>0）的图像上运动.