
科目: 来源: 题型:
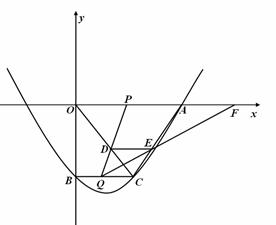
如图,在平面直角坐标系xoy中,抛物线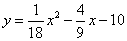 与x轴,y轴的交点分别为点A,点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
与x轴,y轴的交点分别为点A,点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<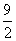 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
查看答案和解析>>
科目: 来源: 题型:
点A(-1,0)B(4,0)C(0,2)是平面直角坐标系上的三点。
① 如图1先过A、B、C作△ABC,然后在在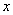 轴上方作一个正方形D1E1F1G1,
轴上方作一个正方形D1E1F1G1,
使D1E1在AB上, F1、G1分别在BC、AC上
② 如图2先过A、B、C作圆⊙M,然后在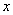 轴上方作一个正方形D2E2F2G2,
轴上方作一个正方形D2E2F2G2,
使D2E2在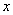 轴上 ,F2、G2在圆上
轴上 ,F2、G2在圆上
③ 如图3先过A、B、C作抛物线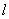 ,然后在
,然后在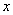 轴上方作一个正方形D3E3F3G3,
轴上方作一个正方形D3E3F3G3,
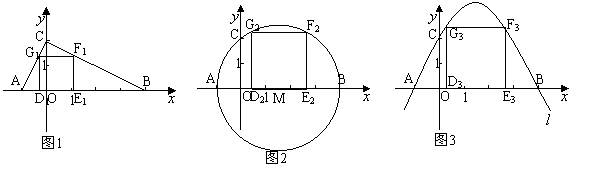
使D3E3在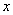 轴上, F3、G3在抛物线上
轴上, F3、G3在抛物线上
请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小
查看答案和解析>>
科目: 来源: 题型:
某校对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分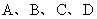 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
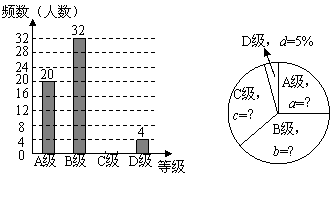

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了__________名同学的体育测试成绩,扇形统计图中A、B、C级所占的百分比分别为a=___________;b= ___________;c=_________;
(2)补全条形统计图;
(3)若该校九年级共有800名同学,请估计该校九年级同学体育测试达标(测试成绩B级以上,含B级)约有___________名.
查看答案和解析>>
科目: 来源: 题型:
随着人民生活水平的不断提高,萧山区家庭轿车的拥有量逐年增加.据统计,某小区2007年底拥有家庭轿车81辆,2009年底家庭轿车的拥有量达到144辆.
(1)若该小区2007年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2010年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目: 来源: 题型:
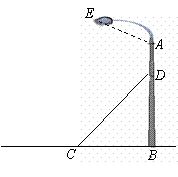
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.
(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,
则灯的顶端E距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400=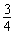 )
)
 |
查看答案和解析>>
科目: 来源: 题型:
数学课上,老师用多媒体给同学们放了由魔术界当红艺人刘谦表演的的神奇的障眼法“硬币穿玻璃”魔术,敏捷的身手、幽默的语言把同学们逗得乐不可支。看完后老师说:“今天我也来当一回魔术师给你们现场表演一个数学魔术。”说完便在黑板上画出下面两个图:
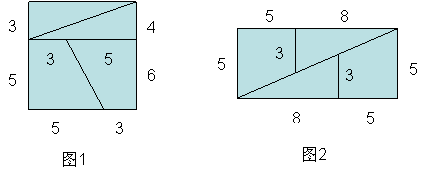

请你借助数学知识帮助同学们分析老师画的这两个图,通过计算验证说明图1到图2的拼接是否可行,若不行请说明理由,并画出正确的拼接图
查看答案和解析>>
科目: 来源: 题型:
已知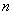 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式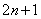 来表示.
来表示.
(1)分解因式: 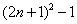 ;
;
(2)我们把所有”奇数的平方减去1”所得的数叫”白银数”,则所有”白银数”的最大公约数是多少?请简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
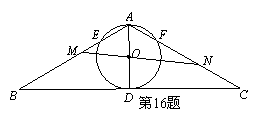
如图,△ABC中,∠B=∠C=30°,AD⊥BC,O是AD上一点(1)若⊙O是△ABC的内切圆,且半径为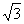 ,则AB=_______;(2)若以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F. 过O点的直线MN分别交线段BE和CF于M,N,且AM:MB=3:5,则AN:NC的值为______________.
,则AB=_______;(2)若以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F. 过O点的直线MN分别交线段BE和CF于M,N,且AM:MB=3:5,则AN:NC的值为______________.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com