不等式组的解集在数轴上表示为（     ）

在平面直角坐标系中,点P(-2,3)的位置在（     ）

如图，已知AB∥CD，∠A=70°，则∠1的度数是（     ）

A. 70°B. 100°C. 110°  D. 130°

已知抛物线y=ax²+x+c（a≠0）经过A（﹣1，0），B（2，0）两点，与y轴相交于点C，该抛物线的顶点为点M，对称轴与BC相交于点N，与x轴交于点D．

（1）求该抛物线的解析式及点M的坐标；

（2）连接ON，AC，证明：∠NOB=∠ACB；

（3）点E是该抛物线上一动点，且位于第一象限，当点E到直线BC的距离为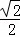时，求点E的坐标；

（4）在满足（3）的条件下，连接EN，并延长EN交y轴于点F，E、F两点关于直线BC对称吗？请说明理由．

如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1.5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．

（1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；

（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？

（3）连接AF，在运动过程中，是否存在某一时刻t，使得S_△AEF=S_{四边形ABOF}？若存在，请求出此时t的值；若不存在，请说明理由．

如图，已知AB，AC分别是⊙O的直径和弦，点G为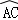上一点，GE⊥AB，垂足为点E，交AC于点D，过点C的切线与AB的延长线交于点F，与EG的延长线交于点P，连接AG．

（1）求证：△PCD是等腰三角形；

（2）若点D为AC的中点，且∠F=30°，BF=2，求△PCD的周长和AG的长．

甲、乙两个商场出售相同的某种商品，每件售价均为3000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一件按原售价收费，其余每件优惠30%；乙商场的优惠条件是：每件优惠25%．设所买商品为x件时，甲商场收费为y₁元，乙商场收费为y₂元．

（1）分别求出y₁，y₂与x之间的关系式；

（2）当甲、乙两个商场的收费相同时，所买商品为多少件？

（3）当所买商品为5件时，应选择哪个商场更优惠？请说明理由．

如图，在梯形ABCD中，AD∥BC，∠ABC=90°，∠BCD=45°，点E在BC上，且∠AEB=60°．若AB=2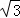，AD=1，求CD和CE的长．（注意：本题中的计算过程和结果均保留根号）

有四张正面分别标有数字2，1，﹣3，﹣4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从四张卡片中随机地摸取一张不放回，将该卡片上的数字记为m，再随机地摸取一张，将卡片上的数字记为n．

（1）请画出树状图并写出（m，n）所有可能的结果；

（2）求所选出的m，n能使一次函数y=mx+n的图象经过第二、三、四象限的概率．

如图，在矩形ABCD中，点E为AB的中点，EF⊥EC交AD于点F，连接CF（AD＞AE），下列结论：

①∠AEF=∠BCE；

②AF+BC＞CF；

③S_△CEF=S_△EAF+S_△CBE；

④若=，则△CEF≌△CDF．

其中正确的结论是　　．（填写所有正确结论的序号）