下列运算正确的是

A． B． C． D．

下面的图形中，既是轴对称图形又是中心对称图形的是       

下列立体图形中，侧面展开图是扇形的是                  

的绝对值是                                        

   A．4             B．          C．          　D．

 问题情境：如图1，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点。

问题探究：（1）在旋转过程中，

①如图2，当AD＝BD时，线段DP、DQ有何数量关系？并说明理由。

②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由。

③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为_______________（直接写出结论，不必证明）

（2）当AD＝BD时，若AB＝20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由。

                图1                 图2                     图3

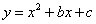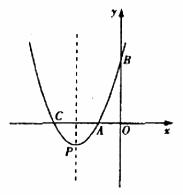
已知抛物线与x轴交于点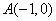、C，与y轴交于点B（0，3），抛物线的顶点为p。

（1）求抛物线的解析式；

（2）若抛物线向下平移k个单位后经过点（－5，6）。

①求k的值及平移后抛物线所对应函数的最小值；

②设平移后抛物线与y轴交于点D，顶点为Q，点M是平移后的抛物线上的一个动点。请探究：当点M在何处时，△MBD的而积是△MPQ面积的2倍？求出此时点M的坐标。

 如图所示，△ABC是等腰三角形，且AC＝BC，∠ACB＝120°，在AB上取一点O，使OB＝OC，以O为圆心，OB为半径作圆，过C作CO∥AB交⊙O于点D，连接BD。

（1）猜想AC与⊙O的位置关系，并证明你的猜想；

（2）试判断四边形BOCD的形状，并证明你的判断；

（3）已知AC＝6，求扇形OBC围成的圆锥的底面圆半径。

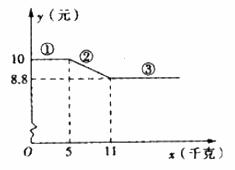
 在某水果店一次性购买A种水果的单价y（元）与购买量x（千克）的函数关系如图所示。

（1）下列关于三段函数图象的说法不正确的是（  ）

A. 第①段函数图象表示数量不多于5千克时，单价为10元。

B. 第③段函数图象表示数量不少于11千克时，单价为8.8元。

C. 第②段函数图象可知：当一次性数量多于5千克但不多于11千克时，每多买1千克，单价就降低1.2元。

（2）求图中第②段函数图象的解析式，并指出x的取值范围。

（3）某天老李计划用90元去该店买A种水果，问老李一次性（或最多）能买回多少千克A种水果？

如图1是一张折叠椅子，图2是其侧面示意图，已知椅子折叠时长1.2米，椅子展开后最大张角∠CBD＝37°，且BD＝BC，AB：BG：GC＝1：2：3，座面EF与地面平行，当展开角最大时，请解答下列问题：

（1）求∠OGF的度数；

（2）求座面EF与地面之间的距离。（可用计算器计算，结果保留两个有效数字，参考数据：sin71.5°≈0.948，cos71.5°≈0.317，tan71.5°≈2.989

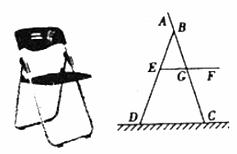
图1             图2

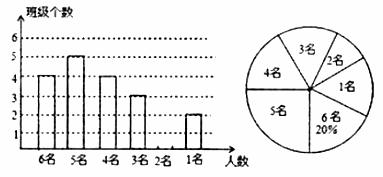
 为响应吉安市2014年创建国家级卫生城市的号召，某校对八年级各班文明行为劝导志愿者人数进行了统计，各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况，并制作如下两幅不完整的统计图。

（1）求该年级平均每班有多少文明行为劝导志愿者？并将条形图补充完整；

（2）该校决定本周开展主题实践活动，从八年级只有2名文明行为劝导志愿者的班级中任选两名，请用列表或画树状图的方法，求出所选文明行为劝导志愿者有两名来自同一班级的概率。