
科目: 来源: 题型:
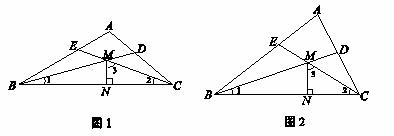
在△ABC中,BD,CE是它的两条角平分线,且BD,CE相交于点M,MN⊥BC于点N.将∠MBN记为∠1,∠MCN记为∠2,∠CMN记为∠3.
(1)如图1,若∠A=110°,∠BEC=130°,则∠2= °,∠3-∠1= °;
(2)如图2,猜想∠3-∠1与∠A的数量关系,并证明你的结论;
(3)若∠BEC= ,∠BDC=
,∠BDC=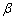 ,用含
,用含 和
和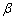 的代数式表示∠3-∠1的度数.(直接写出结果即可)
的代数式表示∠3-∠1的度数.(直接写出结果即可)
查看答案和解析>>
科目: 来源: 题型:
阅读下列材料:
某同学遇到这样一个问题:如图1,在△ABC中,AB=AC,BD是△ABC的高.P是BC边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证: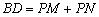 .
.
他发现,连接AP,有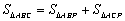 ,即
,即 .由AB=AC,可得
.由AB=AC,可得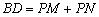 .
.
他又画出了当点P在CB的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是: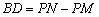 .
.

请回答:
(1)请补全以下该同学证明猜想的过程;
证明:连接AP.
 ∵
∵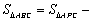 ,
,
∴
 .
.
∵AB=AC,
∴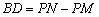 .
.
(2)参考该同学思考问题的方法,解决下列问题:
在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.
①如图3,若点P在△ABC 的内部,则BD,PM,PN,PQ之间的数量关系是: ;

②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是: .
查看答案和解析>>
科目: 来源: 题型:
在一次知识竞赛中,甲、乙两人进入了“必答题”环节.规则是:两人轮流答题,每人都要回答20个题,每个题回答正确得m分,回答错误或放弃回答扣n分.当甲、乙两人恰好都答完12个题时,甲答对了9个题,得分为39分;乙答对了10个题,得分为46分.
(1)求m和n的值;
(2)规定此环节得分不低于60分能晋级,甲在剩下的比赛中至少还要答对多少个题才能顺利晋级?
查看答案和解析>>
科目: 来源: 题型:
如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A( ,
,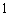 ),
),
B( ,
, ),C(
),C(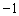 ,
,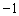 ).将△ABC向右平移5个单位长度,再向下平移4个单位长度,得到△
).将△ABC向右平移5个单位长度,再向下平移4个单位长度,得到△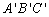 ,其中点
,其中点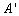 ,
,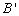 ,
,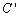 分别为点A,B,C的对应点.
分别为点A,B,C的对应点.
(1)请在所给坐标系中画出△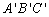 ,并直接写出点
,并直接写出点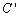 的坐标;
的坐标;
(2)若AB边上一点P经过上述平移后的对应点为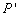 (
(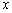 ,
,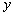 ),用含
),用含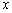 ,
,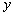 的式子表示
的式子表示
点P的坐标;(直接写出结果即可)
(3)求△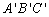 的面积.
的面积.
解:(1)点 的坐标为 ;
的坐标为 ;
(2)点P的坐标为 ;
(3)

查看答案和解析>>
科目: 来源: 题型:
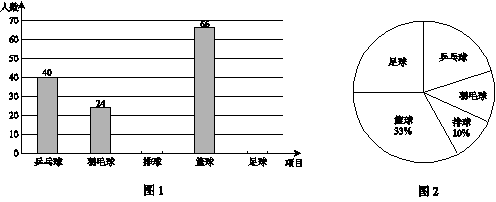
某校学生会为了解该校同学对乒乓球、羽毛球、排球、篮球和足球五种球类运动项目的喜爱情况(每位同学必须且只能从中选择一项),随机选取了若干名同学进行抽样调查,并将调查结果绘制成了如图1,图2所示的不完整的统计图.
(1)参加调查的同学一共有______名,图2中乒乓球所在扇形的圆心角为_______°;
(2)在图1中补全条形统计图(标上相应数据);
(3)若该校共有2400名同学,请根据抽样调查数据估计该校同学中喜欢羽毛球运动的人数.
查看答案和解析>>
科目: 来源: 题型:
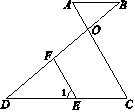
已知:如图,AB∥DC,AC和BD相交于点O, E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠B=40°,∠1=60°,求∠OFE的度数.
(1)证明:
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,直线l经过点A(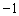 ,
, )点A1,A2,A3,A4,A5,……按如图所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,则A8的坐标为 ;若点An(
)点A1,A2,A3,A4,A5,……按如图所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,则A8的坐标为 ;若点An( 为正整数)的横坐标为2014,则
为正整数)的横坐标为2014,则 = .
= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com