如图把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60°的菱形，剪口与折痕所成的角α的度数应为

  A．15°或30°                     B．30°或45°   

C．45°或60°                     D．30°或60°

若反比例函数y＝的图象经过点(m，3m)，其中m≠0，则此反比例函数的图象在

  A．第一、二象限                   B．第一、三象限   

C．第二、四象限                   D．第三、四象限

如图下列四个几何体，它们各自的三视图（主视图、左视图、俯视图）中，有两个相同而另一个不同的几何体是

A．①②           B．②③         C．②④         D．③④

某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：

这些运动员跳远成绩的中位数和众数分别是

  A．190，200           B．9，9         C．15，9        D．185，200

下列计算中，正确的是

  A．3a－2a＝1                          B．(x＋3y)²＝x²＋9y²

C．(x⁵)²＝x⁷                            D．(－3)^－2＝

下列四个数中，最小的数是

  A．－3                B．－5          C．0            D．

某同学在研究四边形的相关性质时发现，在不改变面积的条件下，一般梯形很难转化为菱形，但有些特殊的梯形通过分割可以转化为菱形．例如以下的等腰梯形就可以转化为菱形（如图1），已知在等腰梯形ABCD中，AD∥BC，AD＝10，CD＝20，∠C＝60°．

（1）求梯形ABCD的面积；

（2）如果将该梯形分割成几块，然后可以重新拼成菱形，试画出变化后的图形（在图1中画出，图形的对应部分标明相同的编号）；

（3）在完成上述任务后，他又试着将梯形的形状变为直角梯形（如图2），其它条件不变，将梯形分成几块．

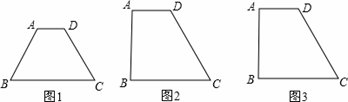①他能拼成一个菱形吗？如果能，请在图2中画出相应的图形；

②他能拼成一个正六边形吗？如果能，请在图3中画出相应的图形．

 对于平面直角坐标系xOy中的点P和⊙O，给出如下的定义：若⊙O上存在两个点A、B，使得∠APB＝60°，则称P为⊙O的关联点．已知点D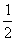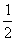（，），E（0，－2），F（2）．

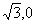（1）当⊙O的半径为1时，①在点D、E、F这三个点中，⊙O的关联点是       ．②过点F作直线l交y轴正半轴于点G，使∠GFO＝30°，若直线l上的点P（m，n）是⊙O的关联点，求m的取值范围；

（2）若线段EF上的所有点都是⊙O的关联点，求⊙O的半径r的取值范围．

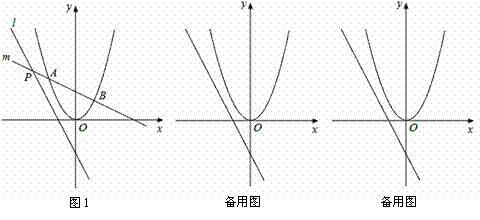
如图1，点P是直线l：y=－2x－2上的点，过点P的另一条直线m交抛物线y=x²于A、B两点．

（1）若A(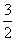－，n)、B(1，1)，求直线m的解析式；

（2）若P(－2，t)，当PA＝AB时，求点A的坐标；

（3）无论点P在l上移动到何处，是否总可以找到这样的直线，使得PA＝AB？若存在，请给予证明，若不存在，请说明理由．

某校决定添置一些跳绳和排球．需要的跳绳的数量是排球数量的3倍，购买的总费用不低于2200元，但不高于2500元．

（1）商场内跳绳的售价为20元/根，排球的售价为50元/个，按照学校所定的费用，有几种购买方案？每种方案中跳绳和排球数量各为多少？

（2）由于购买数量较多，该商场规定20元/根的跳绳可打九折，50元/个的排球可打八折，用（2）中的最少费用，最多还可以多买多少跳绳和排球（按照学校所需跳绳与排球的数量比）？