
科目: 来源: 题型:
定义:如图⑴,若分别以△ABC的三边AC,BC,AB为边向三角形外侧作正方形ACDE,BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形.
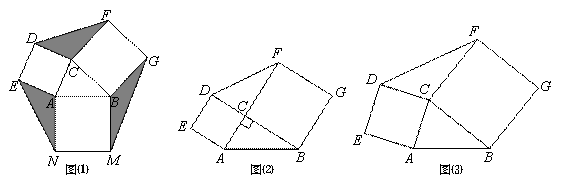 |
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为
S1和S2.
① 如图⑵,当∠ACB=90°时,求证:S1=S2.
② 如图⑶,当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF,△AEN,△BGM的面积和为S,请利用图⑴探究:当∠ACB的度数发生变化时,S的值是否发生变化,若不变,求出S的值;若变化,求出S的最大值.
查看答案和解析>>
科目: 来源: 题型:
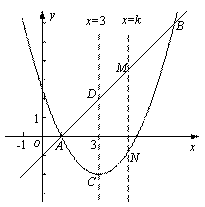
已知抛物线 的顶点为点C.
的顶点为点C.
(1)求证:不论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)若抛物线的对称轴为直线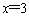 ,求m的值和C点坐标;
,求m的值和C点坐标;
(3)如图,直线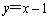 与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线
与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线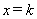 交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.
交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
科目: 来源: 题型:
在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
(1)请你画一个顶点都在格点上,且边长为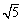 的菱形
的菱形
ABCD,你画出的菱形面积为 ;
(2)若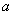 是图中能用网格线段表示的最小无理数,
是图中能用网格线段表示的最小无理数,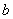 是
是
图中能用网格线段表示的最大无理数,求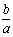 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
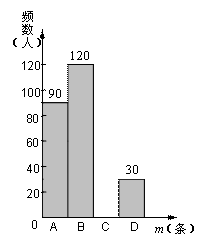
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
 |

|
请你根据以上信息解答下列问题:
(1)在表中:a= ,b= ;
(2)补全频数分布直方图;
(3)参与调查的小聪说,他日均发微博条数是所有抽取的青年人每天发微博数量的中位数,据此推断他日均发微博条数为 级;(填A,B,C,D)
(4)若北京市常住人口中18~35岁的青年人大约有530万人,试估计他们平均每天发微博的总条数.
查看答案和解析>>
科目: 来源: 题型:
已知二次函数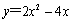 .
.
(1)将此函数解析式用配方法化成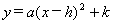 的形式;
的形式;
(2)在给出的直角坐标系中画出此函数的图象(不要求列对应数值表,但要求尽可能画准确);
(3)当0<x<3时,观察图象直接写出函数值y的取值范围: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com