
科目: 来源: 题型:
阅读下列材料并解答相关问题:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图①正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=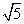 ,BC=
,BC=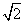 ;
;
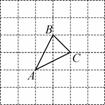


图① 图②
小明同学的做法是:由勾股定理,得AB=AC=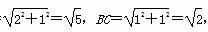 于是画出线段AB、AC、BC,从而画出格点△ABC.
于是画出线段AB、AC、BC,从而画出格点△ABC.
(1)请你参考小明同学的做法,在图②正方形网格(每个小正方形边长为1)中画出格点△A′B′C′(A′点位置如图②所示),使A′B′=A′C′=5,B′C′=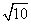 (直接画出图形,不写过程);
(直接画出图形,不写过程);
(2)观察△ABC与△A′B′C′的形状,猜想∠BAC与∠B′A′C′有怎样的数量关系,并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
如图所示,矩形纸片ABCD中,AB=6 cm,BC=8 cm,现将其沿EF对折,使得点C与点A重合,则AF长为( )
A.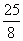 cm B.
cm B.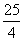 cm C.
cm C.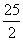 cm D.8
cm D.8
查看答案和解析>>
科目: 来源: 题型:
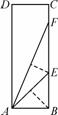
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值,则67.5°角的正切值是( )
A.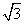 +1 B.
+1 B.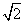 +1 C.2.5
+1 C.2.5  D.
D.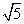
查看答案和解析>>
科目: 来源: 题型:
如图,在△ABC中,∠C=90°,将△ABC沿直线M N翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=2
N翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=2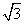 ,则四边形MAB
,则四边形MAB N的面积是( )
N的面积是( )
A.6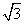 B.12
B.12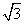 C.18
C.18 D.24
D.24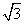
查看答案和解析>>
科目: 来源: 题型:
勾股定理是几何中的一个重要定理, 在我国古算书《周髀算经》中就有“若勾三,股四,则弦五
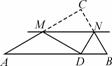
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五 ”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.90 B.100 C.110 D.121
查看答案和解析>>
科目: 来源: 题型:
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边 长是( )
长是( )
A.10 B.4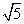 C.10和4
C.10和4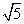 D.10或2
D.10或2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com