
科目: 来源: 题型:
如图4,在△ABC中, AB=AC, CD为∠ACB的平分线,DE∥BC,∠A=40°, 则∠EDC的度数是 ( )
A.30° B.36° C.35° D.54°
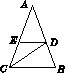
查看答案和解析>>
科目: 来源: 题型:
如图3,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=5 cm,△ADC的周长为17 cm,则BC的长为( )
A.7 cm B.10 cm C.12 cm D.22 cm
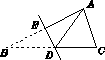
查看答案和解析>>
科目: 来源: 题型:
如图2,△ABC中, ∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于( )
A.44° B. 60° C. 67° D. 77°
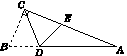
图2 图3 图4
查看答案和解析>>
科目: 来源: 题型:
复习“全等三角形”的知识时,老师布置了一道作业题:“如图16,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图16的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到△ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图17给出证明.
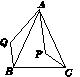
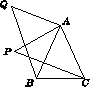
图16 图17
查看答案和解析>>
科目: 来源: 题型:
如图14,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于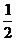 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
查看答案和解析>>
科目: 来源: 题型:
如图13所示,某铁路MN与公路PQ相交于点O,且夹角为90°,某仓库G在A区,到公路和铁路的距离相等,且到铁路的图上距离为1 cm.在图上标出仓库G的位置.
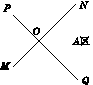
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com