探究问题：圆内有很多关于线段的性质，如果能进行深入的探究，对提高自己的学习能力有很大的帮助。虽然这些知识看起来很复杂，摸不着头脑，但其实，我们完全可以用已经学习过的知识来得到这些新的知识。下面，就请同学们开动脑筋，积极思考，来作一个深入的探究吧。

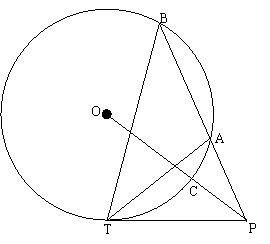
如图所示，PT是圆O的切线，点T是切点，作线段PB与圆O相交，交点为A、B两点，连结TA、OP,OP与圆O相交于点C。

（1）探究∠ATP与∠B之间的关系（提示：过点T作直径与圆相交，连结这个交点与A点）

（2）证明：PT²=PA·PB

（3）如果线段PA=4，AB=5,CP=3，求出圆O的半径。

已知抛物线经过A（-2，0）、B（0，）、C（6，0）三点，连结AB、BC，在抛物线内作平行四边形ABCD，连结BD与x轴交于E点。

（1）求直线BD的解析式；   （2）求此抛物线的解析式；

（3）若抛物线上有一动点P在BC之间移动，那么当它运动到什么位置时，该动点到x轴的距离和到直线BD的距离相等？

如图所示，线段AB是圆O的直径，直线PQ经过圆上一点C，PQ∥AB，连结AC、BC，且AC=BC, AC=5. 点D是圆O上一点，且BD=5.

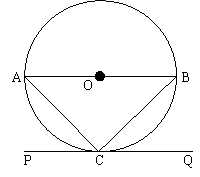（1）求证：PQ是圆O的切线；（2）求∠CBD的大小.

近年来，我市推行了高效课堂教学模式，以“高效率、高效益、高效果”的特点成为了现代教学的新方向. 为了搞好高效课堂教学，班级学生要进行分组，某校九年级一班共有“优生”和“待优生”45名，且“优生”是“待优生”人数的，按相同比例分配到各组，共分成5个组.

（1）每个组分配的“优生”和“待优生”各多少名？

（2）高效课堂的第一个环节是预习，一般为10分钟，“优生”最多只需要5分钟，剩下的时间可以指导本组的“待优生”进行预习，从而使本组的预习在规定时间内完成. 如果没有“优生”的指导，“待优生”预习时间最多不能超过多少分钟，才能使本组的总预习时间不超过规定的总预习时间？

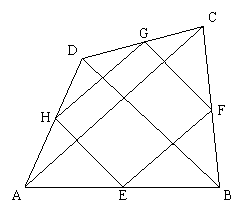
如图，在四边形ABCD中，对角线AC、BD互相垂直，点E、F、G、H分别是边AB、BC、CD、DA的中点，依次连结这四个中点得到四边形EFGH.

（1）求证：四边形EFGH是矩形；

（2）若AC=15，BD=10，求四边形EFGH的周长.

第22届冬奥会于2014年2月7日在俄罗斯的索契市举行. 中国队取得比较好的成绩，美中不足的是没有进入金牌榜前十名.不过，中国队在历届夏季奥运会上表现突出，从1984年美国洛杉矶奥运会至2012年英国伦敦奥运会，共获得金牌数量为201枚，具体每届获得的金牌数如下表所示：

（1）请在上表填写2008年第29届北京奥运会中国所获得的金牌数；

（2）请求出上表中八届奥运会中国所获得的金牌数的平均数（保留整数）；

（3）请将两幅统计图中不完整的部分补充完整；

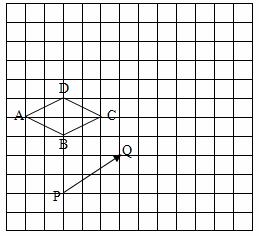
如图所示的正方形网格中，每个小正方形的边长为1. 菱形ABCD的三个顶点A、B、C的坐标为（-5，2）、（-3，1）、（-1，2）.

（1）在网格平面内将菱形ABCD沿PQ平移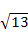个单位长度，请在网格中作出平移后的图形；

（2）写出点D平移后的点的坐标.

先化简，再求值：

，  其中a=3, b=

计算：

如图，点A的坐标为（-1，2），点B的坐标为（2，1），有一点C在x轴上移动，则点C到A、B两点的距离之和的最小值为（    ）

A.        B. 4       C. 3        D.