等腰三角形的顶角为80°，则它的底角的度数是（     ）

A．20°           B．50°           C．60°          D．80°

下列“表情”中属于轴对称图形的是 （     ）

A．         B．        C．        D．

在、、、、、中,分式的个数有（     ）

A、2个          B、3个            C、4个           D、5个

已知直线AB的解析式为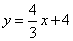：交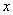轴于点A，交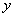轴于点B。动点C从A点出发，以每秒2个单位的速度沿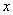轴正方向运动，设运动时间为。

（1）求A、B两点的坐标；

（2）当为何值时，以经过B、C两点的直线与直线AB关于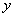轴对称；并求出直线BC的解析式；

（3）直接写出当△ABC为等腰三角形时，对应的值；

（4）在第（2）小题第前提下，在直线AB上是否存在一点P，使得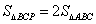，如果不存在，请说明理由；如果存在，请求出此时点P 点坐标。

已知∠ACD=90°，MN是过点A的直线，AC=DC，且DB⊥MN于点B，如图（1）．易证BD+AB=CB，过程如下：

解：过点C作CE⊥CB于点C，与MN交于点E

∵∠ACB+∠BCD=90°，∠ACB+∠ACE=90°，

∴∠BCD=∠ACE．

∵DB⊥MN   ∴∠ABC+∠CBD=90°，

∵CE⊥CB   ∴∠ABC+∠CEA=90°，

∴∠CBD=∠CEA．

又∵AC=DC，

∴△ACE≌△DCB（AAS），

∴AE=DB，CE=CB，

∴△ECB为等腰直角三角形，

∴BE=CB．

又∵BE=AE+AB，

∴BE=BD+AB，

∴BD+AB=CB．

（1）当MN绕A旋转到如图（2）位置时，BD、AB、CB满足什么样关系式，请写出你的猜想，并给予证明．

（2）当MN绕A旋转到如图（3）位置时，BD、AB、CB满足什么样关系式，请直接写出你的结论．

某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进

价、售价如表所示：

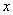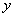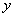（1）设商场购进A型节能台灯为盏，销售完这批台灯时可获利为元，求关于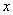的函数解析式？

（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？

如图，有8×8的正方形网格，按要求操作并计算.

（1）在8×8的正方形网格中建立平面直角坐标系，使点A的坐标为（2，4），点B的坐标为（4，2）；

（2）将点A向下平移5个单位，再关于y轴对称得到点C，画出三角形ABC，并求其面积．

如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于O，AC=BD．

求证：（1）BC=AD； （2）△OAB是等腰三角形．