
科目: 来源: 题型:
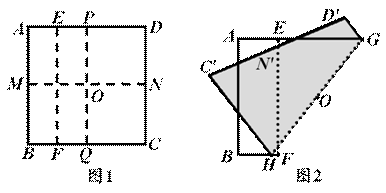
取一张正方形纸片ABCD进行折叠,具体操作过程如下:
第一步:先把纸 片分别对折,使对边分别重合,再展开,记折痕MN,PQ的交点为O;再次对折
片分别对折,使对边分别重合,再展开,记折痕MN,PQ的交点为O;再次对折 纸片使AB与PQ重合,展开后得到折痕EF,如图1;
纸片使AB与PQ重合,展开后得到折痕EF,如图1;
第二步:折叠纸片使点N落在线段EF上,同时使折痕GH经过点O,记点N在EF上的对应点为N',如图2.
解决问题:
(1)请在图2中画出(补全)纸片展平后的四边形CHGD及相应MN,PQ的对应 位置;
位置;
(2)利用所画出 的
的 图形探究∠POG的度数并证明你的结论.
图形探究∠POG的度数并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
(1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问 题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
下面以三等分∠ABC为例说明利 用勾尺三等分锐角的过程:
用勾尺三等分锐角的过程:
第一步:画直线DE使DE//BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B, 同时让点R落在∠ABC的BA边上;
同时让点R落在∠ABC的BA边上;
第三步:标记此 时点Q和点P所在位置,作射线BQ和射线BP.
时点Q和点P所在位置,作射线BQ和射线BP.
请完成第三步操作,图中的三等分线是射线____、____.
(2)在(1)的条件下完成三等分∠ABC的证明过程:
(3 )在(1)的条件下探究:
)在(1)的条件下探究:
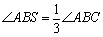 是否成立?如果成立,请说明理由;如
是否成立?如果成立,请说明理由;如 果不成立,请在下图中
果不成立,请在下图中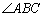 的外部画出
的外部画出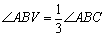 (无需写画法,保留画
(无需写画法,保留画 图痕迹即可).
图痕迹即可).

查看答案和解析>>
科目: 来源: 题型:
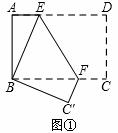
(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点 处,折痕为EF,若∠ABE=20°,那么∠
处,折痕为EF,若∠ABE=20°,那么∠ 的度数为____________.
的度数为____________.
(2)观察发现:
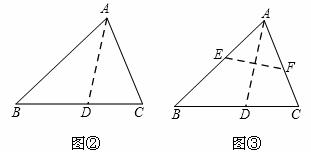
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说 明理由.
明理由.
(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.
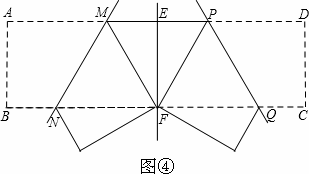
查看答案和解析>>
科目: 来源: 题型:
对一张矩形纸片 ABCD进行折叠,具体操作如下:
ABCD进行折叠,具体操作如下:
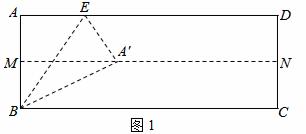
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点 处,并使折痕经过点B,得到折痕BE,同时,得到线段
处,并使折痕经过点B,得到折痕BE,同时,得到线段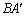 ,
,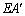 ,展开,如图1;
,展开,如图1;
第三步:再沿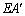 所在的直线折叠,点B落在AD上的点
所在的直线折叠,点B落在AD上的点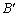 处,
处, 得到折痕EF,同时得到线段
得到折痕EF,同时得到线段 ,展开,如图2
,展开,如图2 .
.
求∠ABE的度数.
查看答案和解析>>
科目: 来源: 题型:
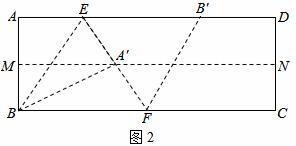
如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是射线CB上任意一点,△ADE是等边三角形,且点D在∠ACB的内部,连接BE.探究线段BE与DE之间的数量关系.请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
 (1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为________,点E落在_________________,容易得出BE与DE之间的数量关系为___________;
(1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为________,点E落在_________________,容易得出BE与DE之间的数量关系为___________;
(2)当点D在 如图3的位置时,请你画出图形,研究
如图3的位置时,请你画出图形,研究 线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
查看答案和解析>>
科目: 来源: 题型:
三等分任意角是三大几何作图不能问题之一,古希腊数学家阿基米德就设计 出了一个巧妙的三等分角的方法:在直尺边缘上添加一点P,命尺端为O(如图①);设所要三等分的角是∠MCN,以C为圆心,OP为半径作半圆交给定角的两边CM、CN于A、B两点;移动直尺,使直尺上的O点在AC的延长线上移动,P点在圆周上移动,当直尺正好通过B点时,连OPB,则有∠AOB=
出了一个巧妙的三等分角的方法:在直尺边缘上添加一点P,命尺端为O(如图①);设所要三等分的角是∠MCN,以C为圆心,OP为半径作半圆交给定角的两边CM、CN于A、B两点;移动直尺,使直尺上的O点在AC的延长线上移动,P点在圆周上移动,当直尺正好通过B点时,连OPB,则有∠AOB= ∠MCN.这种方法由于在直尺上作了一个记号,不符合尺规作图中直尺只能用来连线的规定,因此还不能算是严格意义上的尺规作图.
∠MCN.这种方法由于在直尺上作了一个记号,不符合尺规作图中直尺只能用来连线的规定,因此还不能算是严格意义上的尺规作图.
(1)动手实践操作,用以上方法三等分∠MCN,在图② 中画出图形并
中画出图形并 标明相应字母;
标明相应字母;
(2)请你就阿基米德的作图方法给出证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com