数学课上，李老师出示了如下框中的题目．

小敏与同桌小聪讨论后，进行了如下解答：

（1）特殊情况，探索结论

当点E为AB的中点时，如图1，确定线段AE与DB的大小关系．请你直接写出结论：AE　　DB（填“＞”，“＜”或“=”）．

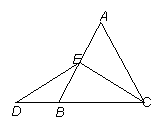图1                          图2

                  （第27题）

（2）特例启发，解答題目

解：题目中，AE与DB的大小关系是：AE　　DB（填“＞”，“＜”或“=”）

理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）

（3）拓展结论，设计新题

在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（画出草图，写出简要过程）．

野营活动中，同学们创造性地选用铁皮代替锅来烙饼．

（1）小明找到一张如图（）的等腰三角形铁皮，用它烙一块与铁皮形状.大小相同的饼．烙好一面后把饼翻身，这块饼仍能正好落在“锅”中，这是因为                              ．

        图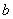（）                图（）                 图（）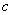

（2）小倩只找到一张如图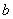（）的直角三角形铁皮，用它烙一块与铁皮形状、大小相同的饼，这块饼翻身就不能正好落在“锅”中．小华将饼切了一刀（沿直线切饼，下同）然后把两小块饼都翻身，它们正好也能落在“锅”中．请你在图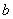（）中画出上述刀痕．

（3）小强最后拿到的是一张如图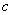（）的三角形铁皮，但它既不是等腰三角形又不是直角三角形，请在图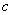（）中画出刀痕的位置（不超过3刀），也能使饼翻身后正好落在“锅”中．（不要写画法，但要作简要文字说明）

 如图所示，这是美国第20任总统加菲尔德证明勾股定理时所采用的图形，是用两个全等的直角三角形和一个等腰直角三角形拼出一个直角梯形．借助这个图形，你能用面积法来验证勾股定理吗？

如图，在□ABCD中，E、F是对角线BD上的两点，且BE=DF，连接AE、CF.请你猜想：AE与CF有怎样的关系？

并对你的猜想加以证明.

如图，在等腰△ABC中，AB＝AC，点O是底边BC的中点，OD⊥AB，

OE⊥AC，垂足分别为D、E．

试说明：OD＝OE．

 如图①，在正方形网格中，每个小正方形的边长为1.在网格中构造格点△ABC（即△ABC 三个顶点都在小正方形的顶点处），AB、BC、AC三边的长分别为、、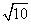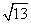，利用网格就能计算三角形的面积.

（1）请你将△ABC的面积直接填写在横线上．__________________．

（2）在图②中画出△DEF，DE、EF、DF三边的长分别为、、.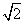

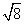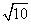①判断三角形的形状，说明理由．

②求这个三角形的面积．

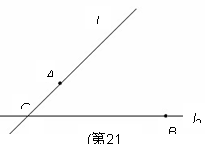
如图，有分别过A、B两个加油站的公路、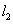相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A.B两个加油站的距离相等，而且P到两条公路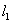、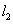的距离也相等.请用尺规作图作出点P（不写作法，保留作图痕迹）．

．

；                       

（－1）⁰+ | 1.4﹣2 |﹣．