已知在△ABC中，AB＝AC，AB的垂直平分线交线段AC于D，若△ABC和        △DBC的周长分别是60 cm和38 cm，则△ABC的腰长和底边BC的长分别是  （    ）

A．24 cm和12 cm      B.16 cm和22 cm 

C．20 cm和16 cm       D．22 cm和16 cm

如图1－75所示，在△ABC中，AD垂直平分扫BC，AC＝EC，点B，D，C，E在同一条直线上，则AB＋DB与DE之间的数量关系是（    ）

A. AB＋DB>DE  B. AB＋DB<DE  C. AB＋DB＝DE    D. 无法判断

已知MN是线段AB的垂直平分线，C，D是MN上任意两点，则∠CAD和∠CBD之间的大小关系是                （    ）

A.∠CAD<∠CBD  B.∠CAD＝∠CBD  C.∠CAD>∠CBD  D.无法判断 

三个牧童A，B，C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时，他们所需走的最大距离（看守点到本区域内最远处的距离）相等．按照这一原则，他们先设计了一种如图1－49（1）所示的划分方案，把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心（对角线交点），看守自己的一块牧场．过了一段时间，牧童B和牧童C又分别提出了新的划分方案．牧童B的划分方案如图1－49（2）所示，三块矩形的面积相等，牧童的位置在三个小矩形的中心．牧童C的划分方案如图1－49（3）所示，把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个要所需走的最大距离相等．

（1）牧童B的划分方案中，牧童       （填“A”“B”或“C”）在有情况时所需走的最大距离较远．

（2）牧童C的划分方案是否符合他们商量的划分原则?为什么?（提示：在计算

    时可取正方形边长为2）

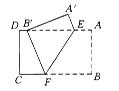
如图1－48所示，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处．

    （1）求证B′E＝BF；

    （2）设AE＝a，AB＝b，BF＝c，试猜想a，b，c之间的一种关系，并给出证明．

如图1－47所示，把矩形ABCD沿对角线BD折叠，点C落在点F处，若AB＝

    12 cm，BC＝16 cm．

    （1）求AE的长；

    （2）求重合部分的面积．

已知等腰三角形ABC中，AB＝AC＝cm，底边BC＝cm，求底边上的高AD

  的长．

如图1－46所示，一艘海轮位于灯塔P的东北方向，距离灯塔海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为      海里（结果保留根号）．

已知△ABC中，边长a，b，c满足a²＝b²＝c²，那么∠B＝        .

在等腰三角形中，腰长是a，一腰上的高与另一腰的夹角是30°，则此等腰三角形的底边上的高是       ．