已知△ABC∽△DEF，相似比为3:5，△ABC的周长为6，则△DEF的周长为____.

如图，⊙M与x轴相交于点A(2,0)，B(8,0)，与y轴相切于点C，则圆心M的坐标是________.

如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，若S△ABC=6，设△ADF的面积为S1，△CEF的面积为S2，则S1-S2的值是_________。

（1）计算: (-1)3×2+-；

（2）化简：.

一批货物要运到某地，货主准备租用汽车运输公司的甲、乙两种货车，

已知前两次租用这两种货车的情况如下表：

现租用该运输公司3辆甲种货车及5辆乙种货车一次刚好运完这批货物，如果按每吨付30元运输费计算，问：货主应该付运输费多少元？

甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相同．比赛结束后，发现参赛学生成绩分别为7分、8分、9分、10分（满分为10分）．

依据统计数据绘制了如下尚不完整的统计图表．

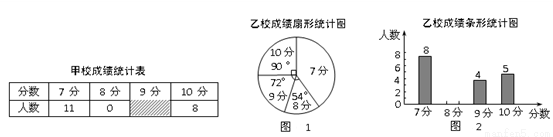
（1）在图1中，“7分”所在扇形的圆心角等于 度；将图2的统计图补充完整；

（2）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数，并从平均分和中位数的角度分析哪所学校的成绩较好；

（3）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校合适？

如图，在楼房AB和塔CD之间有一棵树EF，从楼顶A处经过树顶E点恰好看到塔的底部D点，且俯角α为45°．从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点，且仰角β为30°．已知树高EF=6米，求塔CD的高度．（结果保留根号）

已知，正方形ABCD的边长为6，菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上，AH=2．

（1）如图1，当DG=2，且点F在边BC上时.

求证：① △AHE≌△DGH；

② 菱形EFGH是正方形；

（2）如图2，当点F在正方形ABCD的外部时，连接CF.

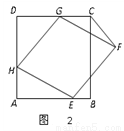
① 探究：点F到直线CD的距离是否发生变化？并说明理由；

② 设DG=x，△FCG的面积为S，是否存在x的值，使得S=1，若存在，求出x的值；若不存在，请说明理由.

如图，已知顶点为A(2,-4)的抛物线经过坐标原点O，经过点A的直线y=kx+2交x轴于点B．

（1）求这条抛物线的函数关系式及点B的坐标；

（2）点P(x,y)是该抛物线的对称轴的左侧、x轴下方一段上的动点，连结 PO，以OQ为底边的等腰△PQO的另一顶点Q在x轴上，过点Q作x轴的垂线交直线AB于点R，连结PR．

设△PQR的面积为S．求S与x之间的函数关系式；

（3）在（2）的条件下，是否存在点P，使得S△PQR=2，若存在，求点P的坐标；若不存在，说明理由．

如图，已知抛物线的顶点坐标为E（1,0），与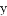轴的交点坐标为（0,1）.

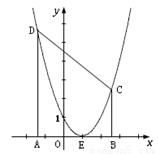
（1）求该抛物线的函数关系式.

（2）A、B是轴上两个动点，且A、B间的距离为AB=4，A在B的左边，过A作AD⊥轴交抛物线于D，

过B作BC⊥轴交抛物线于C. 设A点的坐标为（,0），四边形ABCD的面积为S.

① 求S与之间的函数关系式.

② 求四边形ABCD的最小面积，此时四边形ABCD是什么四边形？

③ 当四边形ABCD面积最小时，在对角线BD上是否存在这样的点P，使得△PAE的周长最小，若存在，请求出点P的坐标及这时△PAE的周长；若不存在，说明理由.