科目： 来源： 题型：解答题

18．（1）问题发现
如图1，△ABC和△BDE均为等边三角形，点A，D，E在同一直线上，连接CD．
填空：
①∠CDB的度数为60°；
②线段AE，CD之间的数量关系为AE=CD．
（2）拓展探究
如图2，△ABC和△DBE均为等腰直角三角形，∠ABC=∠DBE=90°，点A，D，E在同一直线上，BF为△DBE中DE边上的高，连接CD，请判断∠CDB的度数及线段BF，AD，CD之间的数量关系，并说明理由．
（3）解决问题
如图3，在正方形ABCD中，CD=2，CE⊥AE于E，∠BAE=∠BCE，若AE=1，结合（1），（2）的解题经验和结论，请求出点B到AE的距离．

科目： 来源： 题型：填空题

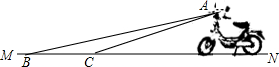17．齐河路路通电动车厂新开发的一种电动车如图，它的大灯A射出的光线AB，AC 与地面MN 所夹的锐角分别为8°和10°，大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m．（不考虑其它因素）
（参考数据：sin8°=$\frac{4}{25}$，tan8°=$\frac{1}{7}$，sin10°=$\frac{9}{50}$，tan10°=$\frac{5}{28}$）

科目： 来源： 题型：解答题

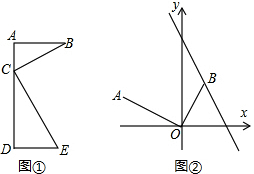16．探究与应用：在学习几何时，我们可以通过分离和构造基本图形，将几何“模块”化．例如在相似三角形中，K字形是非常重要的基本图形，可以建立如下的“模块”（如图①）：
（1）请就图①证明上述“模块”的合理性．已知：∠A=∠D=∠BCE=90°，求证：△ABC∽△DCE；
（2）请直接利用上述“模块”的结论解决下面问题：
如图②，已知点A（-2，1），点B在直线y=-2x+3上运动，若∠AOB=90°，求此时点B的坐标．

科目： 来源： 题型：解答题

15．已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．
（1）如图①，若△ABO是等腰三角形且AO=AB时，求点B的坐标；
（2）如图②，若点C（x，0）且-1＜x＜3，BC⊥AC垂足为点C；
①当x=0时，求tan∠BAC的值；
②若AB与y轴正半轴的所夹锐角为α，当点C在什么位置时tanα的值最大？

科目： 来源： 题型：填空题

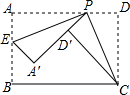14．如图，有一张矩形纸片ABCD，AB=3，BC=4，点P是AD边上任意一点（与点A，D不重合），现将△PCD沿PC翻折，得到△PCD′，再在AB边上选取适当的点E，将△PAE沿PE翻折，得到△PA′E，并使直线PD′，PA重合，线段AE的最大值为$\frac{4}{3}$．

科目： 来源： 题型：填空题

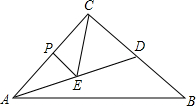13．如图，在Rt△ABC中，∠C=90°，AC=4，BC=5，D是BC边上一点，CD=3，P是AC边上一动点（不与A、C重合），过点P作PE∥BC交AD于点E，将△ABD沿直线AD翻折，得到△AB′D，连接B′C，当∠ACE=∠BCB′时，则AE=$\frac{64}{25}$．

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

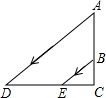9．如图，阳光从教室的窗户射入室内，窗户框AB在地面上的影长DE=1.8m，窗户下檐到地面的距离BC=1m，EC=1.2m，那么窗户的高AB为（　　）

A．

1.5m

B．

1.6m

C．

1.86m

D．

2.16m