
科目: 来源: 题型:填空题
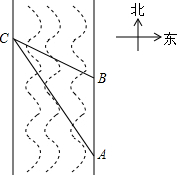 在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)
在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)查看答案和解析>>
科目: 来源: 题型:解答题
 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | -1 | C. | 1±$\sqrt{2}$ | D. | 1$±\sqrt{2}$或-1 |
查看答案和解析>>
科目: 来源: 题型:解答题
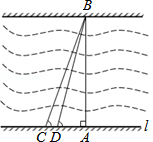 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
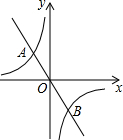 如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.
如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
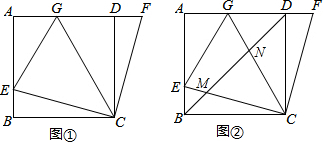
 如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.
如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.查看答案和解析>>
科目: 来源: 题型:填空题
 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com