4．下列说法正确的是（　　）

	A．	掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件
	B．	审查书稿中有哪些学科性错误适合用抽样调查法
	C．	甲乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S甲2=0.4，S乙2=0.6，则甲的射击成绩较稳定
	D．	掷两枚质地均匀的硬币，“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$

3．如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论：（要求用文字语言叙述）垂美四边形两组对边的平方和相等
写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．

2．△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为：垂直．
②BC，CD，CF之间的数量关系为：BC=CD+CF；（将结论直接写在横线上）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2$\sqrt{2}$，CD=$\frac{1}{4}$BC，请求出GE的长．

1．如图，已知AB为半圆O的直径，C为半圆O上一点，连接AC，BC，过点O作OD⊥AC于点D，过点A作半圆O的切线交OD的延长线于点E，连接BD并延长交AE于点F．
（1）求证：AE•BC=AD•AB；
（2）若半圆O的直径为10，sin∠BAC=$\frac{3}{5}$，求AF的长．

20．如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km．一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km．
（1）若轮船照此速度与航向航行，何时到达海岸线？
（2）若轮船不改变航向，该轮船能否停靠在码头？请说明理由．（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）

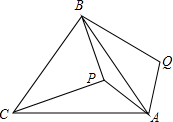19．如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为24+9$\sqrt{3}$．

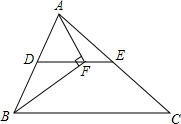18．如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E．若AB=10，BC=16，则线段EF的长为（　　）

A．

2

B．

3

C．

4

D．

5

17．如图，一艘轮船在诲面上由南向北航行，当它行驶到A处时，发现它的东北方向有一座灯塔B，轮船继续向北航行24海里后到达C处，发现灯塔B在它的北偏东75°方向，则此时轮船与灯塔B的距离是（　　）

A．

24$\sqrt{2}$海里

B．

12$\sqrt{2}$海里

C．

24$\sqrt{3}$海里

D．

12$\sqrt{3}$海里

16．我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=$\frac{p}{q}$．例如12可以分解成1×12，2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是12的最佳分解，所以F（12）=$\frac{3}{4}$．
（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数．求证：对任意一个完全平方数m，总有F（m）=1；
（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值．

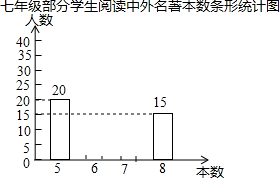15．为响应“全民阅读”号召，某校在七年级800名学生中随机抽取100名学生，对该年级学生在2015年全年阅读中外名著的情况进行调查，整理调查结果发现，学生阅读中外名著的本数，最少的有5本，最多的有8本，并根据调查结果绘制了如图所示的不完整的条形统计图，其中阅读了6本的人数占被调查人数的30%，根据图中提供的信息，补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数．