
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x].
已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x].查看答案和解析>>
科目: 来源: 题型:选择题
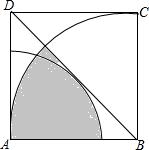 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{π}{2}-1$ | C. | $\frac{5π}{4}-1$ | D. | $\frac{3π}{4}-1$ |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com