2．一个长方形在平面直角坐标系中三个顶点的坐标为（3，2），（-1，2），（3，-1），则第四个顶点的坐标为（-1，-1）．

1．已知直角坐标系中，点P（x，y）满足$\sqrt{x-2}$+（y+3）²=0，则点P坐标为（　　）

A．

（2，3）

B．

（-2，3）

C．

（2，-3）

D．

（2，-3）或（-2，-3）

20．一个正方形的平面展开图如图所示，将它折成正方体后，“保”字对面的字是碳．

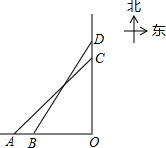19．如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，此时测得轮船乙在甲的东北方向，轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45km/h和36km/h，经过0.1h，轮船甲行驶至B处，轮船乙行驶至D处，此时测得轮船乙在甲的北偏东32°，此时B处距离码头O多远？（结果保留一位小数）（参考数据：sin32°≈0.53，cos32°≈0.85，tan58°≈1.60，tan32°≈0.625）

18．（1）计算：|-4|-2016⁰-$\frac{\sqrt{3}}{3}$cos30°
（2）解方程：$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$．

17．探究：如图1和2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD上，∠EAF=45°．
（1）①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，则能证得
EF=BE+DF，请写出推理过程；
②如图2，若∠B、∠D都不是直角，则当∠B与∠D满足数量关系∠B+∠D=180°时，仍有EF=BE+DF；
（2）拓展：如图3，在△ABC中，∠BAC=90°，AB=AC=2$\sqrt{2}$，点D、E均在边BC上，且∠DAE=45°．若BD=1，求DE的长．

16．计算：-2²+$\sqrt{4}$-（$\sqrt{3}$）⁰．

15．某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
（1）操作发现：
在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是①②③④（填序号即可）
①AF=AG=$\frac{1}{2}$AB；②MD=ME；③整个图形是轴对称图形；④MD⊥ME．
（2）数学思考：
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量关系和位置关系？请给出证明过程；
（3）类比探索：
在任意△ABC中，仍分别以AB、AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：等腰直角三角形．

14．如图，在玲玲家住宅楼CD的前面新建了一个大型商场AB，当光线与地面的夹角是22°时，商场在玲玲家楼上留下高2m的影子CE；而当光线与地面的夹角是45°时，商场楼顶A在地面上的影子F与墙角C有13m的距离（B、F、C在一条直线上）．求商场AB的高度．（参考数据：sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈$\frac{2}{5}$）

13．计算：2^-2$-\sqrt{（-2）^{2}}$+6sin45°-$\sqrt{18}$．