10．把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．
如：①用配方法分解因式：a²+6a+8，
解：原式=a²+6a+8+1-1=a²+6a+9-1=（a+2）（a-4）
②M=a²-2ab+2b²-2b+2，利用配方法求M的最小值，
解：a²-2ab+2b²-2b+2=a²-2ab+b²+b²-2b+1+1=（a-b）²+（b-1）²+1
∵（a-b）²≥0，（b-1）²≥0
∴当a=b=1时，M有最小值1．
请根据上述材料解决下列问题：
（1）在横线上添加一个常数，使之成为完全平方式：x²-$\frac{2}{3}$x+$\frac{1}{9}$．
（2）用配方法因式分解：x²-4xy+3y²．
（3）若M=$\frac{1}{4}$x²+2x-1，求M的最小值．
（4）已知x²+2y²+z²-2xy-2y-4z+5=0，则x+y+z的值为4．

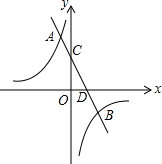9．如图，在平面直角坐标系xOy中，一次函数y=k₁x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A（-1，6）和点B（3，m），与y轴交于点C，与x轴交于点D．
（1）求一次函数y=k₁x+b和反比例函数y=$\frac{{k}_{2}}{x}$的表达式；
（2）点P是双曲线y=$\frac{{k}_{2}}{x}$上的一点，且满足S_△PCD=S_△DOC，求点P的坐标．

8．从5，6，7这三个数字中，随机抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是$\frac{1}{3}$．

7．下列说法正确的是（　　）

	A．	“任意画出一个圆，它是中心对称图形”是随机事件
	B．	为了解我省中学生的体能情况，应采用普查的方式
	C．	天气预报明天下雨的概率是99%，说明明天一定会下雨
	D．	任意掷一枚质地均匀的硬币10次，正面朝上的次数不一定是5次

6．一个不透明的袋子中有1个红球，2个黄球，3个白球，除颜色不同外，其他各方面都相同，现从中随机摸出一个球，这球是黄球概率为$\frac{1}{3}$．

5．如图，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（-1，0）、B（3，0），交于点C（0，-3），设该抛物线的顶点坐标为D，连接AC．

（1）求抛物线的解析式及顶点D的坐标；
（2）在抛物线的对称轴上存在一点P，使△PAC的周长最小，请求出点P的坐标；
（3）在抛物线上是否存在一点M，使S_△MAC=2S_△BCD？若存在，求出点M的坐标；若不存在，请说明理由．

4．在一个不透明的布袋中，放入分别标注1、-2、3三个不同数字的小球，小球除了数字不同外，其余都相同．小明闭上眼睛先把小球搅均，再从该布袋中摸出第一个小球，记小球上的数字为A，把球重新放回布袋中搅均，摸出第二个小球，记小球上的数字为B．
（1）求小明第一次摸出的小球上的数字为“负数”的概率；
（2）求两次摸出的小球上的数字均是一元一次不等式2x+3＞0的解的概率．

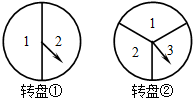3．某班举行联欢会，规定每个同学同时转动转盘①与转盘②（它们分别被二等分和三等分）．若两个转盘停止后，指针所指的数字之积为奇数，则这个同学要表演唱歌节目；若数字之积为偶数，则要表演其它节目．试求出转动转盘的同学表演唱歌节目的概率．（用树状图或列表方法求解）

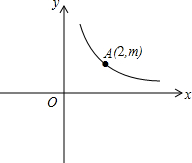2．在平面直角坐标系xOy中，反比例函数y=$\frac{k}{x}$（k＞0）的图象经过点A（2，m），连接OA，在x轴上有一点B，且AO=AB，△AOB的面积为2．
（1）求m和k的值；
（2）若过点A的直线与y轴交于点C，且∠ACO=30°，请直接写出点C的坐标．

1．从1，2，3，4四个数中任取一个数作为AC的长度，又从4，5中任取一个数作为BC的长度，AB=6，则AB、AC、BC能构成三角形的概率是$\frac{5}{8}$．