
科目: 来源: 题型:选择题
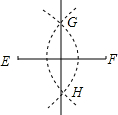 任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )| A. | △EGH为等腰三角形 | B. | △EGF为等边三角形 | ||
| C. | 四边形EGFH为菱形 | D. | △EHF为等腰三角形 |
查看答案和解析>>
科目: 来源: 题型:解答题
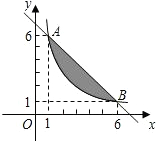 如图,A、B两点在函数y=$\frac{y}{x}$(x>0)的图象上.
如图,A、B两点在函数y=$\frac{y}{x}$(x>0)的图象上.查看答案和解析>>
科目: 来源: 题型:填空题
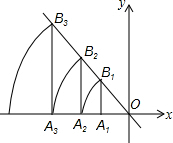 如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).查看答案和解析>>
科目: 来源: 题型:填空题
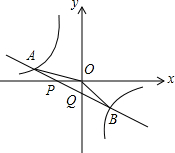 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b$>\frac{{k}_{2}}{x}$的解集是x<-2或0<x<1,其中正确的结论的序号是②③④.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
查看答案和解析>>
科目: 来源: 题型:解答题
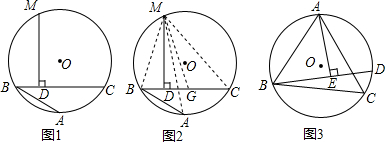
查看答案和解析>>
科目: 来源: 题型:选择题
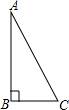 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
查看答案和解析>>
科目: 来源: 题型:解答题
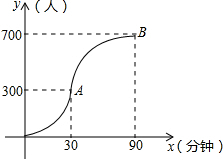 科技馆是少年儿童节假日游玩的乐园.
科技馆是少年儿童节假日游玩的乐园.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com