
科目: 来源: 题型:选择题
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 26 | 36 | 22 | 22 | 24 | 31 | 21 |
| A. | 中位数是22 | B. | 平均数是26 | C. | 众数是22 | D. | 极差是15 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 抛掷2枚正方体骰子,都是6点朝上 | |
| C. | 经过有交通信号灯的路口,遇到红灯 | |
| D. | 任意画一个三角形,其内角和是360° |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
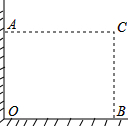 在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.查看答案和解析>>
科目: 来源: 题型:解答题
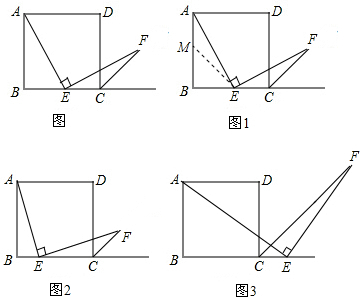
查看答案和解析>>
科目: 来源: 题型:解答题
 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):| 项目人员 | 阅读能力 | 思维能力 | 表达能力 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com