
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
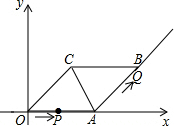 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.查看答案和解析>>
科目: 来源: 题型:解答题
 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
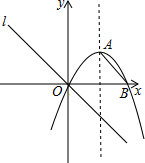 如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.
如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com