
科目: 来源: 题型:选择题
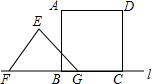 如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )
如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )| A. | 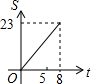 | B. | 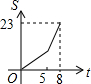 | C. | 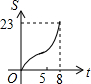 | D. | 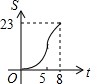 |
查看答案和解析>>
科目: 来源: 题型:选择题
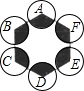 如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )
如图,正六边形的边长为10,分别以正六边形的顶点A、B、C、D、E、F为圆心,画6个全等的圆.若圆的半径为x,且0<x≤5,阴影部分的面积为y,能反映y与x之间函数关系的大致图形是( )| A. | 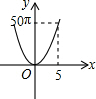 | B. | 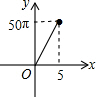 | C. | 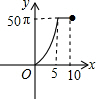 | D. | 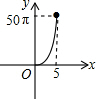 |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:选择题

| A. | PA+AB | B. | PA-AB | C. | $\frac{AB}{PA}$ | D. | $\frac{PA}{AB}$ |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 我省居民原来用电价格为0.45元/kw•h.2016年1月起,试行居民用电峰谷分时电价政策:峰段指8时-22时,电价为0.5元/kw•h;谷段指22时-次日8时,电价为0.3元/kw•h.符合条件的居民用户可以自愿选择,向当地电网企业提出申请,由电网企业免费安装峰谷分时电能表.
我省居民原来用电价格为0.45元/kw•h.2016年1月起,试行居民用电峰谷分时电价政策:峰段指8时-22时,电价为0.5元/kw•h;谷段指22时-次日8时,电价为0.3元/kw•h.符合条件的居民用户可以自愿选择,向当地电网企业提出申请,由电网企业免费安装峰谷分时电能表.| 月平均用电量(单位kw•h) | |
| 峰段 | 谷段 |
| 120kw•h | 80kw•h |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 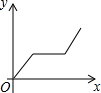 | B. | 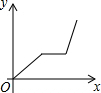 | C. | 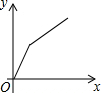 | D. | 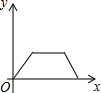 |
查看答案和解析>>
科目: 来源: 题型:解答题
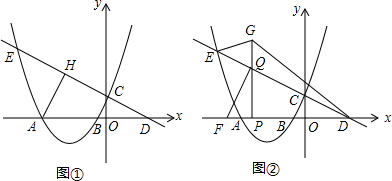
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com