科目： 来源： 题型：填空题

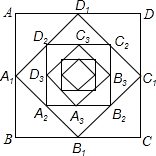14．连结正方形四边中点所构成的正方形，我们称其原正方形的中点正方形，如图，已知正方形ABCD的中点正方形是A₁B₁C₁D₁，再作正方形A₁B₁C₁D₁的中点正方形A₂B₂C₂D₂，…这样不断地作下去，第n次所做的中点正方形 A_nB_nC_nD_n，若正方形ABCD的边长为1，则第10次所作的中点正方形边长为$\frac{1}{32}$，若设中点正方形 A_nB_nC_nD_n的面积为S_n，则S₁+S₂+S₃+…+S₁₀=$\frac{1023}{1024}$．

科目： 来源： 题型：填空题

科目： 来源： 题型：解答题

12．如图，已知抛物线经过原点o和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=-2x-1经过抛物线上一点B（-2，m）且与y轴交于点C，与抛物线的对称轴交于点F．
（1）求m的值及该抛物线对应的解析式；
（2）P（x，y）是抛物线上的一点，若S_△ADP=S_△ADC，求出所有符合条件的点P的坐标；
（3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形．若能，请直接写出点M的运动时间t的值；若不能，请说明理由．

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

10．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
（1）概念理解：
如图1，在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）问题探究：
①小红猜想：对角线互相垂直的“等邻边四边形”一定是菱形．她的猜想正确吗？请说明理由．
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=4，BC=2，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结BA′，CC′，小红要使平移后的四边形A′BCC′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

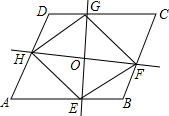8．如图，过?ABCD的对角线AC的中点O任作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE，有下面四个结论，①OH=OF；②∠HGE=∠FGE；③S_{四边形DHOG}=S_{四边形BFOE}；④△AHO≌△AEO，其中正确的是（　　）

A．

①③

B．

①②③

C．

②④

D．

②③④

科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

6．如图，已知直线a∥b，直线l与直线a相交于点P，与直线b相交于点Q，且MP⊥直线l，若∠1=58°，则∠2的度数为32°．

科目： 来源： 题型：填空题