
科目: 来源: 题型:填空题
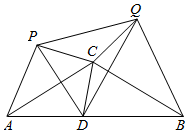 如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:查看答案和解析>>
科目: 来源: 题型:填空题
 某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.
某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | m-2>n-2 | B. | $\frac{m}{2}$>$\frac{n}{2}$ | C. | m2>n2 | D. | 2m+1>2n+1 |
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,在一个足够大的桌面上,画满了等距的平行线,间距为2厘米,现有一个半径为r厘米的圆形硬币,若事件“将该硬币任意掷于桌面上,硬币压到所画直线”是必然事件,则r的取值可以是2.
如图,在一个足够大的桌面上,画满了等距的平行线,间距为2厘米,现有一个半径为r厘米的圆形硬币,若事件“将该硬币任意掷于桌面上,硬币压到所画直线”是必然事件,则r的取值可以是2.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.
如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com