10．已知一组数据：5，9，13，13，5．下列说法正确的是（　　）

A．

平均数是9

B．

极差是4

C．

众数是9

D．

中位数是13

9．阅读理解并填空：
（1）为了求代数式x²+2x+3的值，我们必须知道x的值．若x=1，则这个代数式的值为6；若x=2，则这个代数式的值为11，…，可见，这个代数式的值因x的取值不同而变化（填“变化”或“不变”）．尽管如此，我们还是有办法来考虑这个代数式的值的范围．
（2）数学课本第105页这样写“我们把多项式a²+2ab+b²及a²-2ab+b²叫做完全平方式”．在运用完全平方公式进行因式分解时，关键是判断这个多项式是不是一个完全平方式．同样地，把一个多项式进行部分因式分解可以来解决代数式值的最大（或最小）值问题．例如：x²+2x+3=（x²+2x+1）+2=（x+1）²+2，因为（x+1）²是非负数，所以，这个代数式x²+2x+3的最小值是2，这时相应的x的值是-1∵．
尝试探究并解答：
（3）求代数式-x²+14x+10的最大（或最小）值，并写出相应的x的值．
（4）求代数式2x²-12x+1的最大（或最小）值，并写出相应的x的值．
（5）已知y=$\frac{1}{2}$x²-3x-$\frac{3}{2}$，且x的值在数1～4（包含1和4）之间变化，求这时y的变化范围．

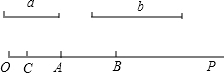8．根据所示图形填空：
已知线段a、b，画一条线段，使它等于2a-b．
解：①画射线OP；
②在射线OP上顺次截取OA=AB═a；
③在线段OB上截取BC=b．
线段OC就是所要画的线段．

7．若x²+mx+9是关于x的完全平方式，则m的值为（　　）

A．

3

B．

3或-3

C．

6

D．

6或-6

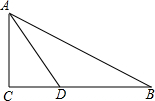6．如图，在△ABC中，∠C=90°，AD平分∠BAC与BC边交于点D，BD=2CD，若点D到AB的距离等于5cm，则BC的长为（　　）

A．

5

B．

10

C．

15

D．

无法确定

5．下列事件为必然事件的是（　　）

	A．	任意买一张电影票，座位号是奇数
	B．	三根长度为4cm，4cm，8cm的木棒能摆成三角形
	C．	打开电视机，正在播放纪录片
	D．	两边及其夹角对应相等的两个三角形全等．

4．如图，在同一直角坐标坐标系中作出两个一次函数的图象，则利用图象可以解下列二元一次方程组的是（　　）

	A．	$\left\{\begin{array}{l}{x+y-2=0}\\{3x-2y-1=0}\end{array}\right.$		B．	$\left\{\begin{array}{l}{x+y-2=0}\\{2x-y-1=0}\end{array}\right.$
	C．	$\left\{\begin{array}{l}{2x-y-1=0}\\{3x+2y-5=0}\end{array}\right.$		D．	$\left\{\begin{array}{l}{2x-y-1=0}\\{3x-2y-1=0}\end{array}\right.$

3．两个多边形相似的条件是（　　）

	A．	对应角相等		B．	对应角相等且对应边成比例
	C．	对应角相等或对应边成比例		D．	对应边成比例

2．下面的图形是天气预报中的图标，其中既是轴对称图形又是中心对称图形的是（　　）

A．

霾

B．

大雪

C．

浮尘

D．

大雨

1．阅读并填空：
如图，六年级第二学期我们已经学过用直尺、圆规作线段中点的方法：
（1）以点A为圆心，以大于$\frac{1}{2}$AB的长a为半径作弧；以点B为圆心，以a为半径作弧，两弧分别相交于点E、F；
（2）作直线EF，交线段AB于点C．点C就是所求线段AB的中点，并说明这种做法正确的理由．
解：连接AE、BE、AF、BF．
在△AEF和△BEF中，
EF=EF（公共边），
AE=BE（画弧时所取的半径相等），
AF=BF（画弧时所取的半径相等）．
所以△AEF≌△BEF （SSS）．
所以∠AEF=∠BEF （全等三角形的对应角相等）．
又因为AE=BE，
所以AC=BC （等腰三角形三线合一）．
即点C是线段AB的中点．