
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
| 练习罚球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 罚中次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 罚中频率 |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 如图,某小区计划用18m的铁栅栏两面靠墙(墙足够长)围成一个矩形车棚ABCD,为了方便存车,在CD(CD>2)边上开了一个2m宽的门EF(门不是用铁栅栏做成的),设边BC的长为xm,车棚面积为ym2.
如图,某小区计划用18m的铁栅栏两面靠墙(墙足够长)围成一个矩形车棚ABCD,为了方便存车,在CD(CD>2)边上开了一个2m宽的门EF(门不是用铁栅栏做成的),设边BC的长为xm,车棚面积为ym2.查看答案和解析>>
科目: 来源: 题型:解答题
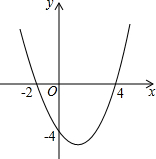 二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题:
二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题:查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com