练习册

  • 练习册
  • 试题
    相关习题
     0  287644  287652  287658  287662  287668  287670  287674  287680  287682  287688  287694  287698  287700  287704  287710  287712  287718  287722  287724  287728  287730  287734  287736  287738  287739  287740  287742  287743  287744  287746  287748  287752  287754  287758  287760  287764  287770  287772  287778  287782  287784  287788  287794  287800  287802  287808  287812  287814  287820  287824  287830  287838  366461 

    科目： 来源： 题型：解答题

    19．如图，现在有以下几个条件：
    ①AB=CD；②AC=BD；③∠A=∠D；④∠ABC=∠DCB；
    请从以上4个条件中，挑选出2个作为条件，1个作为结论组成一个正确的命题，并写出证明过程．
    条件：①②；
    结论：③；
    证明：
    在△ABC与△DCB中，
    ∵$\left\{\begin{array}{l}AB=DC\\ AC=DB\\ BC=BC\end{array}\right.$，
    ∴△ABC≌△DCB（SSS），
    ∴∠A=∠D．．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    18．解方程：x2-144=0．

    查看答案和解析>>

    科目： 来源： 题型：解答题

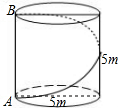    17．壁虎在一座油罐的下底边沿A处．它发现在自己的正上方──油罐上边缘的B处有一只害虫．壁虎决定捕捉这只害虫．为了不引起害虫的注意，它故意不走直线，而是绕着油罐，沿着一条螺旋路线，从背后对害虫进行突然袭击如图．结果，壁虎的偷袭得到成功，获得了一顿美餐．请问：壁虎沿着螺旋线爬行是最短的路程吗（线段AB除外）？

    查看答案和解析>>

    科目： 来源： 题型：选择题

    16．某校八年级（1）班师生从学校出发到10千米外的植物园游玩，一部分同学先步行，1小时后，其余同学骑自行车从学校出发，虽然“…”，求步行同学的速度，设步行同学的速度为xkm/h，则可列方程为$\frac{10}{x}$-$\frac{10}{3x}$=1+0.5，根据此情景和所列方程，题中“…”表示缺失的条件应该为（　　）
    A．骑自行车同学的速度比步行同学的速度多3km/h，步行的同学先到达植物园0.5h
    B．骑自行车同学的速度是步行同学的速度3倍，步行的同学先到达植物园0.5h
    C．骑自行车同学的速度是步行同学的速度3倍，骑自行车的同学先到达植物园0.5h
    D．骑自行车同学的速度比步行同学的速度多3km/h，骑自行车的同学先到达植物园0.5h

    查看答案和解析>>

    科目： 来源： 题型：选择题

    15．下列各式中，计算正确的是（　　）
    A．$\frac{{x}^{6}}{{x}^{3}}$=x2B．$\frac{{a}^{2}-3a}{9-{a}^{2}}$=$\frac{a}{a+3}$
    C．$\frac{{a}^{2}-{b}^{2}}{（a-b）^{2}}$=$\frac{a+b}{a-b}$D．$\frac{4{x}^{2}y{z}^{2}}{12{x}^{2}{y}^{2}z}$=$\frac{4z}{12y}$

    查看答案和解析>>

    科目： 来源： 题型：解答题

    14．如图所示，在道路OA、OB的交叉区域内有M、N两所学校，现要在此区域内建一图书馆P，使它到两条道路的距离相等，并且到两所学校的距离也相等，求P点位置．（不写作法，保留作图痕迹）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．如图所示，点A、B在直线MN上，AB=11cm，⊙A、⊙B的半径均为1cm，⊙A以每秒2cm 的速度自左向右运动，与此同时，⊙B的半径也在不断增大，其半径r（cm）与时间t（秒）之间的关系式为r=1+t（t≥0），当⊙A出发后几秒两圆外切？在运动过程中，两圆会内切吗？如果会，求⊙A的运动时间，如果不会，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    12．几何计算题：
    （1）如图，⊙O中，$\widehat{AB}=\widehat{AC}$，∠C=75°，求∠A的度数．
    （2）⊙O的半径为13cm，弦AB∥CD，AB=24cm，CD=10cm，求AB和CD的距离．
    （3）三角形三边长为5cm，12cm，13cm，以这个三角形三个顶点为圆心的三个圆两两外切，则这三个圆的半径分别是多少？

    查看答案和解析>>

    科目： 来源： 题型：解答题

    11．二次根式计算：
    （1）$\sqrt{9a}+\sqrt{25a}$；
    （2）$\sqrt{75}-\sqrt{54}+\sqrt{96}-\sqrt{108}$；
    （3）（$\sqrt{48}+\frac{1}{4}\sqrt{6}$）÷$\sqrt{27}$；
    （4）（2$\sqrt{3}$$+\sqrt{6}$）（2$\sqrt{3}$$-\sqrt{6}$）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    10．如图，四边形ABCD的四个顶点的坐标分别为A（-5，1），B（-2，1），C（-2，5），D（-5，4），分别画出与四边形ABCD关于y轴和x轴对称的图形．

    查看答案和解析>>

    同步练习册答案