
科目: 来源: 题型:解答题
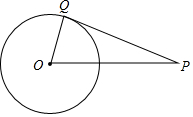 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2cos$\frac{180°}{n}$ | B. | 2sin$\frac{180°}{n}$ | C. | 2tan$\frac{180°}{n}$ | D. | 2cot$\frac{180°}{n}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
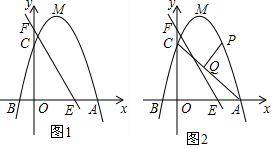
查看答案和解析>>
科目: 来源: 题型:解答题
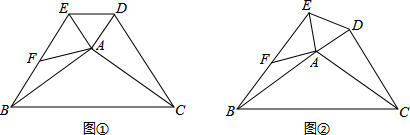
查看答案和解析>>
科目: 来源: 题型:解答题
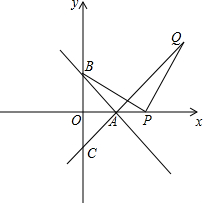 直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.查看答案和解析>>
科目: 来源: 题型:解答题
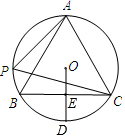 如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.
如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.查看答案和解析>>
科目: 来源: 题型:解答题
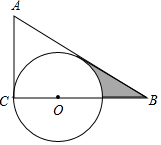 已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.
已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.查看答案和解析>>
科目: 来源: 题型:填空题
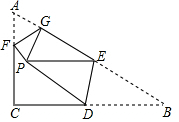 如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.
如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com