8．阅读下列材料：
根据联合国《人口老龄化及其社会经济后果》中提到的标准，当一个国家或地区65 岁及以上老年人口数量占总人口比例超过7%时，意味着这个国家或地区进入老龄化．从经济角度，一般可用“老年人口抚养比”来反映人口老龄化社会的后果．所谓“老年人口抚养比”是指某范围人口中，老年人口数（65 岁及以上人口数）与劳动年龄人口数（15-64 岁人口数）之比，通常用百分比表示，用以表明每100 名劳动年龄人口要负担多少名老年人．
以下是根据我国近几年的人口相关数据制作的统计图和统计表．
2011-2014 年全国人口年龄分布图

2011-2014 年全国人口年龄分布表

	2011年	2012年	2013年	2014年
0-14岁人口占总人口的百分比	16.4%	16.5%	16.4%	16.5%
15-64岁人口占总人口的百分比	74.5%	74.1%	73.9%	73.5%
65岁及以上人口占总人口的百分比	m	9.4%	9.7%	10.0%

根据以上材料解答下列问题：
（1）2011 年末，我国总人口约为13.47亿，全国人口年龄分布表中m的值为9.1%；
（2）若按目前我国的人口自然增长率推测，到2027 年末我国约有14.60 亿人．假设0-14岁人口占总人口的百分比一直稳定在16.5%，15-64岁人口一直稳定在10 亿，那么2027 年末我国0-14岁人口约为2.409亿，“老年人口抚养比”约为22%；（精确到1%）
（3）2016 年1 月1 日起我国开始实施“全面二胎”政策，一对夫妻可生育两个孩子，在未来10年内，假设出生率显著提高，这不会（填“会”或“不会”）对我国的“老年人口抚养比”产生影响．

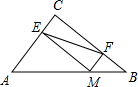7．如图，在△ABC中，AC=9，BC=12，AB=15，点M为AB边上的点，过M作ME⊥AC交AC于E，MF⊥BC交BC于F，连接EF，则EF的最小值为$\frac{36}{5}$．

6．定义运算：x?y=$\left\{\begin{array}{l}{x（1+y）}&{（x≥y）}\\{y（1-x）}&{（x＜y）}\end{array}\right.$，则（-1）?2=4．

5．如图，在△ABC中，AD⊥BC，垂足为D，E为AC上一点，BE交AD于点F，且BF=AC，FD=CD，AD=4，则AB=4$\sqrt{2}$．

4．如图，在△ABC中，AD⊥BC，垂足为D，E为AC上一点，BE交AD于F，且BF=AC，FD=CD，AD=3，求AB的长．

3．方法介绍：
同学们，生活中的很多实际问题，我们往往抽象成数学问题，然后通过数形结合建立数学模型的方式来解决．
例如：学校举办足球赛，共有五个球队参加比赛，每个队都要和其他各队比赛一场，问该学校一共要安排多少场比赛？
这是一个实际问题，我们可以在平面内画出5个点（任意3个点都不在同一条直线上），如图①所示，其中每个点各代表一个足球队，两个队之间比赛一场就用一条线段把他们连起来，其中连接线段的条数就是安排比赛的场数．这样模型就建立起来了，如何解决这个模型呢？由于每个队都要与其他各队比赛一场，即每个点都要与另外4点连接一条线段，这样5个点应该有5×4=20条线段，而每两个点之间的线段都重复计算了一次，实际只有10条线段，所以学校一共要安排10场比赛．
学以致用：
（1）根据图②回答：如果有6个班级的足球队参加比赛，学校一共要安排15场比赛；
（2）根据规律，如果有n个班级的足球队参加比赛，学校一共要安排$\frac{n（n-1）}{2}$场比赛．
问题解决：
（1）小明今年参加了学校新组建的合唱队，老师让所有人每两人相互握手，认识彼此（每两人之间不重复握手）．小明发现所有人握手次数总和为36次，那么合唱队有多少人？
（2）A、B、C、D、E五人参加一次会议，见面时他们相互握手问好，每两人之间不重复握手．已知A已经握了4次，B已经握了3次，C已经握了2次，D已经握了1次，请利用图③分析E已经和哪些人握手了．
问题拓展：
根据上述模型的建立和问题的解决，请你提出一个问题，并进行解答．

2．王强在电脑上进行高尔夫球的模拟练习，从原点处按函数关系式y=-$\frac{1}{5}$x²+$\frac{8}{5}$x击球，球正好进洞中，y（m）是球的飞行高度，x（m）是求飞出的距离．
（1）画出函数y=-$\frac{1}{5}$x²+$\frac{8}{5}$x的图象；
（2）从图象上看，高尔夫球的最大飞行高度是多少？球的起点与洞之间的距离是多少？

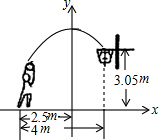1．如图，运动员甲在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5m时，达到最大高度3.5米，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05米．
（1）建立如图所示的直角坐标系，求抛物线的解析式．
（2）该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？
（3）运动员乙跳离地面时，最高能摸到3.3m，问：在（2）的条件下，运动员乙在运动员甲与篮板之间的什么范围内能在空中截住球？

14．如图，已知，D为△ABC中BC边上一点，∠B=∠C=∠DAB，且∠ADC=∠DAC，求∠BAC的度数．

13．在Rt△ABC中，∠ACB=90°，CD⊥AB于D．若BC=3，AC=4，则tan∠BCD的值为$\frac{3}{4}$．